1. 引言
不同于阿克曼转向方式,差速转向车辆对两侧车轮施加不同驱动和制动力,通过控制两侧车轮的速度差来实现转向功能。最初,差速转向系统主要用于履带式车辆,后来,凭借简单、紧凑、可靠、高效、机动性强以及能够实现原地转向等优点,差速转向系统逐渐在轮式车辆中得到广泛应用。随着自动驾驶技术的发展,无人驾驶的轮式差速转向车辆在军事、抢险救灾等领域展现了广阔的应用前景,受到国内外学者的普遍关注。
在无人驾驶轮式差速转向车辆研究领域,轨迹跟踪控制是关键研究方向之一,尤其是在复杂野外环境下,实现高精度轨迹跟踪是确保全地形车辆安全行驶和顺利完成任务的基础 [1] 。文献 [2] 对差速转向轮式车辆进行动力学分析,设计了纵向力矩与转向两侧轮速差解耦控制的控制器,完成对参考轨迹的跟踪。文献 [3] 对四轮差速转向车进行运动学分析,通过考虑内外侧车轮的真实速度与转弯半径间的关系,对控制器进行优化设计。文献 [4] 对电传动履带车的运动特性进行分析,并实现了差速转向控制。文献 [5] 对模型预测控制在无人驾驶车辆轨迹跟踪问题中的应用进行了全面综述。文献 [6] 提出了基于非线性模型预测控制的滚动预测范围估计方法,有效地提高了跟踪精度。文献 [7] 在线性车辆模型的基础上建立了mpc路径跟踪控制器,并对前轮偏角进行约束,提高了车辆稳定性。文献 [8] 根据模糊算法调节mpc的权重值,提高了不同曲率下的路径跟踪算法的鲁棒性。文献 [9] 考虑路面附着系数对控制器的影响,设计了自适应预测时域,在添加侧偏角约束后取得了较好效果。文献 [10] 设计了自适应采样周期的路径跟踪控制器,对采样周期进行动态规划,很好地兼顾了实时性和跟踪精度。
在经典模型预测控制算法中,目标函数的状态量权重和控制量权重系数一般为定常值,当轨迹跟踪误差变大时,无法及时做出响应,不利于车辆参考轨迹的高精度跟踪。为解决这个问题,对目标车辆进行运动学和动力学分析,并将动力学分析结果作为mpc目标函数的约束条件。此外,提出一种目标函数状态权重与控制权重参数动态调节方法,以轨迹跟踪误差为依据,不断调整状态量和控制量权重,以提高跟踪精度。最后的仿真实验验证了改进mpc轨迹跟踪控制器的高精度与可靠性。
2. 差速车辆模型
2.1. 运动学模型
如所示,水陆两栖救灾差速转向八轮车的同一侧车轮由同一个电机驱动,具有相同转速。
图中:oxy为大地惯性坐标系;差动车的位置和姿态可以定义为oxy坐标系中的
,θ为车辆的航向角;假设质心位于车辆几何中心o,oxy为车体参考坐标系
分别为差动车辆的纵向速度、横向速度、横摆角速度;
分别为左右两侧车轮速度;b为两侧车轮中心距。则车辆的运动学微分方程可表示为:
. kinematic model of differential vehicle
. 差速车辆运动学模型
(1)
根据所选择的控制量,以及差速转向特性可化简为:
(2)
式中:
。
2.2. 动力学模型
为了简化车辆的动力学模型,假设车辆行驶在绝对平坦的道路上并仅受到道路作用在车辆上的力,忽略由空气动力学产生的各种力与力矩作用。动力学模型如所示。
根据车体受力分析得到车身动力学微分方程:
(3)
(4)
(5)
式中:m为整车质量;
、
、
分别为差动车辆的纵向速度、横向速度、横摆角速度;
、
、
、
分别代表第i轴的左、右轮接地处所受到的纵向和横向力;
为绕z轴的转动惯量;b为左右车轮的轮距;
、
、
、
分别为各轮轴距离质心的距离,在质心位置前的为正,在质心后的为负。
. vehicle body dynamic model
. 车身动力学模型
对车轮进行受力分析,假设每个车轮与地面的接触情况相同,车轮动力学模型如。
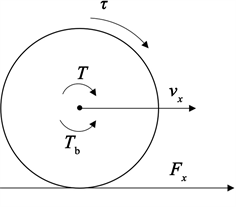
. wheel dynamic model
. 车轮动力学模型
以一侧车轮建立动态运动微分方程,如下所示:
(6)
式中:
为车轮的转动角速度;
分别表示左、右侧车轮;r为车轮的有效半径;
为电机到车轮的传动比;
为轮胎滑移率;t为驱动力转矩;
为制动力转矩,
为单个车轮的转动惯量。
车辆受到的力最终可以归于车轮与地面之间的相互产生的轮胎力,在理想条件下,不考虑离心力对其的影响,对于全驱动车的附着力为:
(7)
式中:
为车辆附着力;g为重力加速度;μ为路面附着系数;α为坡度角(在此忽略不计)。
3. 基于模型预测控制的轨迹跟踪
3.1. 轨迹跟踪控制器设计
模型预测控制器的核心思想是将实际控制问题转化为一个目标函数,在满足一系列约束条件的情况下,通过最优化求解方法,计算出未来一段时间内的最佳控制序列。随后,将该控制序列的首个控制输入应用于被控系统,以实现对系统的精确控制。无人差速转向车辆系统可以抽象为:
(8)
其中,
为系统状态量,
表示车辆几何中心o在大地坐标系下的位置,
为控制量。定义跟踪误差
,
,
为参考路径给出的目标位置,
为期望航向角。经过前向欧拉法离散后,误差跟踪模型为:
(9)
式中:k表示第k个求解时刻;t为离散时间步长。
用公式(1)的运动学方程表示离散后的误差跟踪模型为:
(10)
设计的目标函数需要确保目标车辆能够快速、平稳、精确地跟踪规划模块提供的参考轨迹。为此,需要将系统状态偏差以及控制输入纳入目标函数中,其表达方式如下:
(11)
其中,
(12)
式中:q和r为权重矩阵,
为控制增量,
为预测时域。状态误差
。
式(11)右侧的第一项表示系统在跟踪参考轨迹方面的性能,而第二项则表示对控制输入变化的约束。这个目标函数的优点在于其容易转化为标准的二次规划形式。
3.2. 约束条件
约束条件可以分为两类:等式约束和不等式约束。等式约束通常用于描述系统的预测模型,即用于表达相邻时刻之间的状态转移关系。而不等式约束则一般基于车辆的执行能力来限定控制量、控制量增量等的取值范围。其对控制量约束表示为:
(13)
对控制增量约束表示为:
(14)
式中:
、
分别为控制量的下限值、上限值;
、
分别为控制增量的下限值、上限值。控制量与控制增量的约束通过式(3)~(7)所示的动力学模型进行计算。
为了便于控制器设计,本文基于以下假设对车辆动力学模型进行简化:1) 车辆的纵向速度保持恒定不变;2) 假设车辆的轮胎工作在线性区域内;3) 仅考虑车辆在平面内做平面运动,不考虑立体运动;4) 在分析中忽略了空气阻力、滚动阻力等阻力因素的影响;5) 不考虑车辆的侧倾和俯仰运动;6) 假设车辆质心处纵向速度等于车辆两侧轮胎接地点的纵向速度均值;7) 忽略传动比和传动损失。控制增量限制的表达式如下:
(15)
式中:μ为路面附着系数,
,为左右侧车轮纵向力。
则目标函数转化为标准二次规划形式:
(16)
式中:
,
。
3.3. 控制器参数优化
在mpc轨迹跟踪控制器中,q矩阵用于衡量系统状态与参考轨迹之间的误差对性能指标的影响,r矩阵用于衡量控制输入变化对性能指标的影响。
通过调整q和r矩阵的参数,可以使mpc控制器在实时运行中更好地满足性能要求。如果q矩阵中的元素较大,控制器将更注重减小状态误差,但这可能导致控制输入变化较大。相反,如果r矩阵中的元素较大,控制器将更注重减小控制输入的变化,但可能导致状态误差相对较大。因此,通过调整这些参数,可以平衡状态误差和控制输入,以实现更好的控制性能。
q和r矩阵动态参数调整规则如式(17)所示:
,
(17)
式中:q、r分别代表q和r矩阵的权重参数;
为实际轨迹与参考轨迹之间的误差(这里指与参考轨迹的欧式距离);x为最小误差参考量;a、b、c、d分别为给定比例系数。可以看出:以实际轨迹和规划轨迹的误差为参考量,当误差大于一定值时提高状态矩阵的权重,以达到提高跟踪精度的目的;当误差小于一定值时,提高控制矩阵的权重,可以使控制量更加趋于稳定。
4. 仿真实验与分析
为了验证算法的有效性与跟踪精度,在matlab平台下进行仿真实验,差速转向车辆的具体参数如所示,mpc控制器算法参数如所示。将mpc控制器设计问题转化为标准二次规划问题,并使用matlab提供的quadprog函数在线求解。
. simulate vehicle model parameters
. 仿真车辆模型参数
. mpc controller parameters
. mpc控制器参数
式(17)关于动态调节参数设置为,
,
,
,
。以双移线为参考轨迹,参考速度为10 m/s,路面附着系数为0.8。分别使用改进mpc方法与经典mpc方法进行相同工况下的对比仿真实验。
跟踪结果如所示:
. trajectory tracking effect diagram
. 轨迹跟踪效果图
横向跟踪误差与航向角误差分别如(a)和(b)所示:
(a) (b)
. lateral error diagram and heading error diagram
. 横向误差与航向误差
所示为轨迹跟踪仿真结果。
. simulation experiment effect statistics
. 仿真实验效果统计
通过、和可以看出:通过动态调节权重参数,针对差速转向车辆设计的改进mpc控制器比经典mpc控制器的横向跟踪误差降低35.3%,航向跟踪误差降低3%,跟踪精度有明显提高。
5. 结论
针对自动驾驶水陆两栖救灾车辆的轨迹跟踪问题,建立了差速转向八轮车运动学模型和动力学模型,并结合动力学约束设计了改进mpc轨迹跟踪控制器,该控制器以车辆实时跟踪误差为依据对目标函数中的状态量与控制量权重矩阵系数进行动态调节,有效提高了参考轨迹的横向及航向跟踪精度。通过验证可得出,动态的调节控制器参数可以有效地提高控制精度。