1. 引言
1887年,赫兹(h.r. hertz)用莱顿瓶作放电实验,发现了电磁波,并观察到光电效应的早期征兆。电磁波的发现开创了麦克斯韦(james clerk maxwell)电磁场理论发展应用的新纪元,而光电效应的问世又使经典理论遇到了前所未有的麻烦,120多年过去了,至今还没有文献应用经典理论成功地解释它。
1905年爱因斯坦(albert einstein)用光量子理论成功地解释了光电效应,使光的粒子性得到了空前的发展。然而,已经发现:在碱金属和少数逸出功较大的金属(如钼、镍、钽、钨、钡等)中存在选择性光电效应[1] ;2009年发现了金也存在选择性光电效应[2] ;还有文献揭示了铅存在多峰值选择性光电效应,并显示出铅原子核外不同壳层轨道具有不同逸出功[3] ,这又使不完备的光量子理论难以解释。
1940年世界上第一台电子感应加速器的问世,标志着人类应用电磁场加速电子已经从理论变成了现实,至今还在应用和发展着。其理论和实践表明:运动着的带电粒子在电磁场中一定受到变化磁场产生的洛伦兹力的驱动作用,同时还一定受到由变化磁场激发产生的涡旋电场的电场力的驱动作用,本文把运动带电粒子在电磁场中同时受到这两个力的驱动作用简称为电磁场驱动。
原子系统主要由电子和原子核组成,电子绕核转动。处于光波、热辐射等电磁场中的原子系统,电子和原子核都一定受到电磁场驱动,电子和原子核的能量和运动轨迹都要被迫发生改变。然而,到目前为止100多年来,还没有找到文献应用电磁场驱动研究电子和原子核的受迫运动,研究解释光电效应,研究解释单峰值和多峰值选择性光电效应。在波动学说不能解释光电效应的书籍文献的论述中,都没有抓住光波的电磁场本质,没有抓住光波的振幅实质上是变化磁场和涡旋电场的强度,是这两个场对电子的驱动,这是电动力驱动,不是机械力驱动。而19世纪末20世纪初那时的解释,把光波理解为机械波,以机械波的振幅推动周围媒质作相应运动,来理解光波的振幅推动电子作相应运动、使电子运动幅度达到逸出进行解释[4] [5] ,也许是由于当时对电磁场还非常生疏,才没能抓住电磁场的本质。本文吸取前人之鉴,抓住绕原子核旋转电子在光波电磁场中一定受到洛伦兹力和涡旋电场力驱动作用这一关键之处,以这两个驱动力为外动力,建立和求解了绕原子核旋转电子的运动微分方程,得到了电子受迫吸收能量解、受迫运动轨迹解,以光的电磁场波动理论、以数学语言解释了光电效应,解释了单峰值和多峰值选择性光电效应,以及原子核外不同壳层轨道具有不同的逸出功。
2. 单峰值和多峰值选择性光电效应等物理现象
2.1. 爱因斯坦对光量子的困惑包含一场新的革命
1905年,科学巨星爱因斯坦(albert einstein)将量子力学奠基人普朗克(max planck)1900年提出的能量子学说应用于光学,大胆假设光线是由一个一个不连续的光量子(现在称为光子)组成,每一个光量子具有hν的能量,“这些能量子能够运动,但不能再分割,而只能整个地被吸收或产生出来[6] 。”以此为基础创立了光电效应方程,成功地解释了在当时实验条件下发现的光电效应的实验规律。这一成果,十年后得到了国际物理学界的普遍认同和赞誉。然而在对光量子学说的赞扬声中,爱因斯坦是清醒的,直到晚年,1951年12月12日在给老朋友贝索的信中,坦言了自己内心对光量子的困惑和对盲从者的严厉责备:“整整50年的自觉思考没有使我更接近于解答‘光量子是什么’这个问题。的确,现在每一个无赖都相信,他懂得它,可是他在欺骗他自己[7] 。”然而,如何看待爱因斯坦这段话中50年来追求真理、追求完美的“自觉思考”以及50来年不懈的奋斗,却常常引起一些人的误解,正如当代著名的数学、理论物理学家罗杰彭罗斯1997年12月在《爱因斯坦奇迹年》一书的序言中写道:“经常引起另一种表现的悖论:为什么在理解量子现象方面爱因斯坦起初与同时代人相比处于如此领先的优势地位,而在量子论的随后发展中他却落后于他们?确实,当量子论采取在20世纪20年代最终出现的形式时,爱因斯坦甚至从未接受过这种量子论。许多人可能认为,爱因斯坦是受他‘过时的’实在论的观点阻碍,而尤其如玻尔之所以能向前推进则恰恰是因为他否认在分子、原子和基本粒子这样的量子水平上这类东西真正作为‘物理实在’而存在。可是,很清楚,爱因斯坦在1905年能够作出这些根本性的进展,主要取决于坚信在分子和亚分子层次上物理实体的实际存在性。这些重要倾向在本书的五篇论文中显得特别明显。”罗杰彭罗斯接着写道:“是否真如玻尔的追随者认为的那样,在任何重要的意义上爱因斯坦都犯了深刻的‘错误’?我不认为如此。我自己就坚决地站在爱因斯坦一边,相信亚微观粒子的实在性,相信今天的量子力学基本上是不完备的。我也主张,关于这种实在性的本质的一些关键性见识尚有待发现,这只有通过深刻分析量子论的基本原理和爱因斯坦自己的广义相对论的基本原理间的表现冲突才能最终显现。在我看来,只有掌握了这些知识,并加以适当运用,支配微观世界的量子论定律同支配宏观世界的广义相对论定律之间带有根本性的紧张关系才能得以解决。怎样才能成功地实现,只有时间,而且,我相信,一场新的革命将会作出回答——或许是另一个奇迹年[8] !”这段话指明了爱因斯坦的困惑不是没有道理的,而是包含着“一场新的革命”,并明确指出:“今天的量子力学基本上是不完备的”。
从爱因斯坦坦言困惑又过了60多年,关于光子与电子之间的能量转换,二者之间的能量在极短的一瞬间如何具体地进行转移,这样一个非常关键的问题,至今还是停留在“只能整个地被吸收或产生”上,其发展也只是“部分吸收”、“双光子吸收”、“多光子吸收”等等,还没有文献资料详细描述“吸收或产生”那一瞬间的暂态物理过程、以及电子吸收光子后的运动轨迹、产生光电效应的运动轨迹等等。随着时间的推移和对光电效应的深入实验和研究,又陆续发现了一些新的困惑,发现了用光量子学说难以解释的碱金属甚至金阴极单峰值、多峰值选择性光电效应等物理现象。这不能不引起深思。现将这些困惑的物理现象简述如下。
2.2. 金属单峰和多峰值选择性光电效应曲线及γ截止限
众所周知:爱因斯坦光电效应方程是直线方程,非曲线方程。因此不可能出现选择性光电效应峰值曲线,也不会在频率高端γ频段出现截止。而已经由实验发现的金属单峰和多峰值曲线及γ截止限是与爱因斯坦光电效应直线方程不一致的,是光量子理论无法解释的。请看以下的例子:
(1) 刘元震等编著《电子发射与光电阴极》一书中指出了在碱金属和极少数逸出功大的金属(如钡、钼、镍、钨等)中发现了光电效应存在选择性峰值[1] (见图1)。图中的单峰值曲线明显不同于hν线性曲线,尤其是铯、铷、钾的曲线在波长缩短(频率升高)的方向有形成另一峰的趋势,其中钾最为明显。对选择性光电效应产生的原因,书中作了如下论述:“在一定频率范围内,金属中吸收了光量子能量后激发到真空能级以上的自由电子数目随着频率的增高而增大,而自由电子吸收光量子的概率在频率较高时将随着频率的增高而减少,这两个因素共同作用,造成了在某频率时光电子发射的峰值。”这段话没有数学式的表达,难以说明单峰曲线,更难以说明多峰值曲线。
(2) 袁铮等《金阴极的选择性光电效应》论文中测出了非碱金属、且在空气中十分稳定的au阴极在200~340 nm (3.66~6.22 ev)紫外波段与线性单调递增有突出偏离的单峰选择性光谱响应特性曲线(图2),由图可知,“au阴极光谱响应并不是单调递增,而是在5.72 ev处呈现一个峰值,光子能量大于5.72 ev时,光谱响应迅速衰减[2] 。”由于袁铮等的实验光源频带窄,没能测出多峰值选择性光电效应曲线,但这单峰值曲线明显不同于hν线性曲线。
(3) 丁富荣等编著的《辐射物理》一书在讨论光电效应的段落中提供了两幅图,明显显示出多峰值选择性光电效应曲线(图3),不过书中是以多吸收限的文字表述的。众所周知,吸收能量是产生光电效应的前提条件,不吸收光能就不会产生光电效应。因此,吸收能量的峰值隐含着光电效应的峰值。书中指出:光电截面σph随光子能量的增加而减小,并非线性增加。图3(b)“给出了铅的光电截面在l吸收限附近的变化情况。铅中k壳层的吸收限为88.3 kev,而l、m层电子能级存在子壳层结构,各子壳层能级稍有差异,因而光电截面在l吸收限和m吸收限附近存在着精细结构。例如。铅的l层有三个吸收限:l3
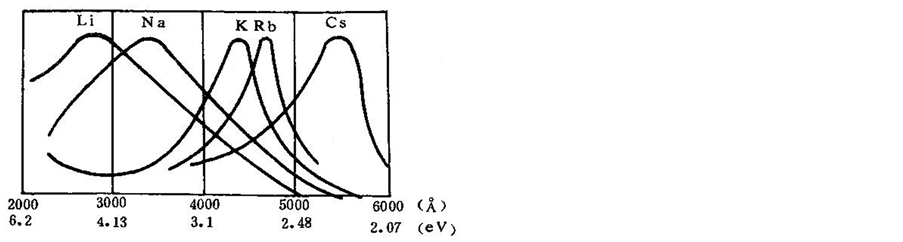
. selective spectral photoemission curves of several alkali metals
图1. 几种碱金属的选择性光谱特性曲线
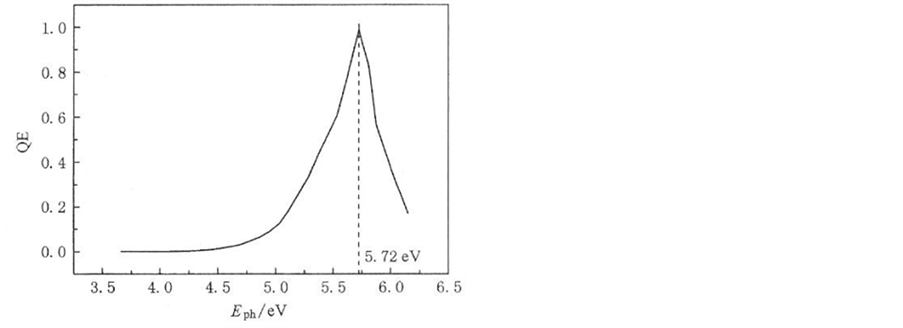
. selective spectral photoemission curves of au photocathode
图2. au阴极的单峰选择性光谱响应特性曲线
吸收限为13.06 kev,l2吸收限为15.26 kev,l1吸收限为15.91 kev[9] 。”观察图可知,这种尖锐突变的吸收限是σph的峰值点,隐含的是光电效应的峰值点。图中的三个吸收限有可能形成选择性光电效应曲线的三个峰值点,“在l吸收限和m吸收限附近存在着精细结构”则可能是精细的更多的峰值结构。
关于γ截止点,图3(a)“显示了在几种不同吸收物质中的光电截面与γ光子能量的关系。σph随光子能量eγ的增大而减少,随靶物质z的增加而增大。当光子能量eγ < 100 kev时,光电截面随eγ的变化出现特征性的突变,这种尖锐的突变点称为吸收限[10] 。”从图3(b)上还可以看出当光子能量eγ < 100 kev时,出现了光电截面σph的截止点,也就是光电效应的截止点,本文将其称之为γ截止限。
(4) 徐克尊等主编的《近代物理学》一书中提供了“铅的吸收系数与入射光子能量关系”图(图4),由图可见,“有明显的吸收峰,称为吸收边,图上有k吸收边、l吸收边、m吸收边对应于不同壳层的
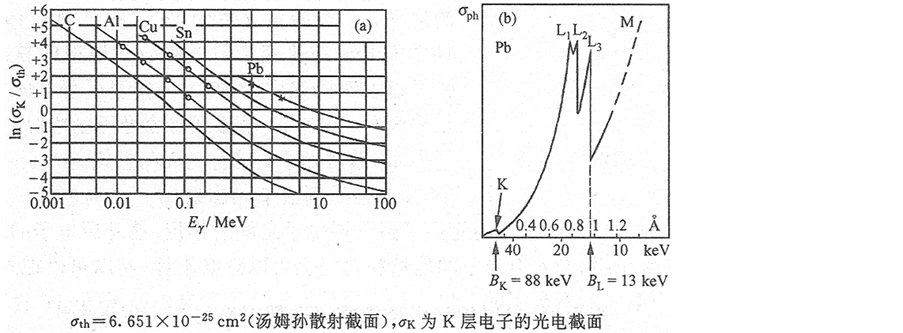
. γ cutoff limits and many peak selective photoemission
图3. 光电截面γ截止限和多峰值选择性光电效应
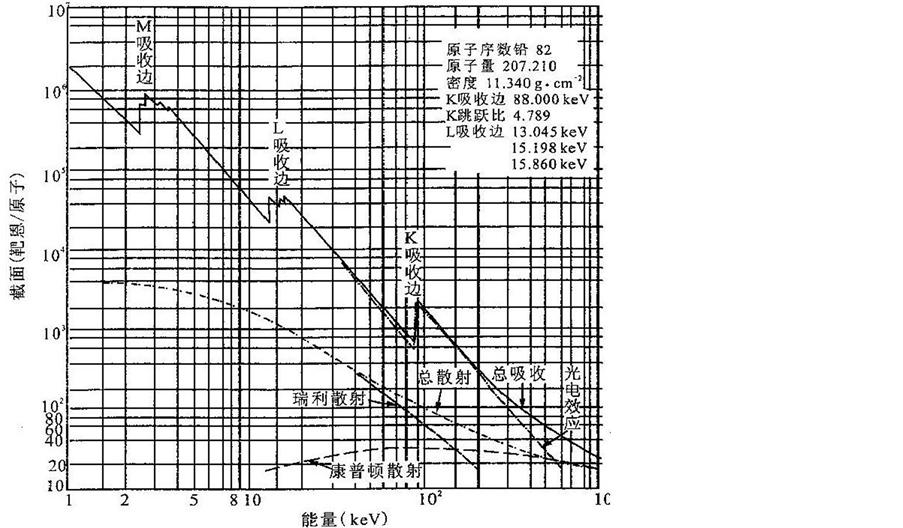
. γ cutoff limits and many peak selective photoemission of ph
图4. 铅的多峰值选择性光电效应和γ截止限
吸收。…l吸收边又精细地分为三个:li,lii和liii;m吸收边分为5个[3] 。”这种多峰吸收有可能形成多峰值选择性光电效应,图中还可以看出γ截止限。
(5) 黄昆著《固体物理学》[11] 第九章“固体中的光吸收”中“激子光吸收”一节提供了“cu2o的激子吸收光谱”也显示出多峰吸收现象(图5)。
以上例子可以说明一些金属光电效应具有单峰和多峰值选择性特性及γ截止限,这是应用光量子学说难以解释的。
2.3. 轨道选择性光电效应
从图3b和图4还可以看出:l壳层轨道的3个峰明显高于k壳层的峰,而m壳层的5个峰明显高于l壳层。这说明光电效应对轨道也具有选择性,对某一个壳层轨道吸收光波能量最少。这种对轨道具有选择性光电效应的现象还没有找到有关文献提出过,应用光量子学说也是难以解释的,但物理学必须要直面这种实验事实。
2.4. 原子核外不同壳层轨道具有不同的逸出功
从图3b和图4还可以看出:l壳层轨道的3个峰、k壳层的峰、m壳层的5个峰分别具有不同的能量值,如果把各壳层的精细结构测出来,这不同的能量值还会更多。这不同的值表示具有不同的逸出功,这就意味着同一种物质不是只有单值一种逸出功,而是具有多值多种逸出功,不同的壳层轨道分别具有不同的逸出功。这种物质逸出功的多值特性也没有找到有关文献提出过,应用光量子学说亦难以解释,但物理学也必须要直面这种实验事实。
面对以上多峰值选择性光电效应(或多峰吸收)和γ截止限、轨道选择性、多值逸出功,很需要当今物理学作出圆满的解释。
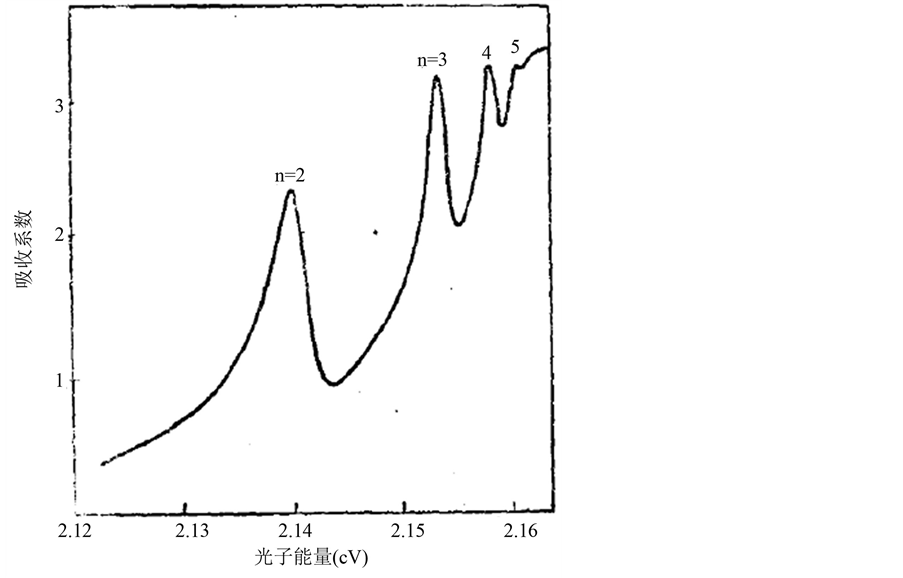
. multiple peaks selective photoemission curves of cu2o under the 77k
图5. 77k下cu2o的激子多峰吸收谱线
3. 核外电子受电磁场两力驱动微分方程的建立和求解
为解释多峰值选择性光电效应,本文先研究核外电子在光波电磁场驱动下、如何摆脱原子核的束缚、成为光电子。为此首先建立核外电子和原子核之间库仑力运动方程,再建立电子受电磁场涡旋电场力和洛伦兹力两外力驱动的微分方程。
3.1. 核外电子和原子核之间库仑力运动方程
电子与电子之间存在库仑斥力,电子与原子核之间存在库仑引力。应用静电场高斯定理,可以求出原子核外任一电子ej(从低能级往高能级按顺序数第j个)所受到的所有斥力与引力的合力fc为(详见附录1):

式中:e:电子电荷量的绝对值;ε0:真空介电常量;r:以原子核的中心为极点,从极点指向轨道上运动电子ej就是矢径r;a:常数,a = 2(z − j) 1,其中z:原子核电荷数。
考虑电子在绕核旋转运动中的阻力或能量损耗,该力与运动速度成正比,设阻力系数为k1,则该力为-k1υ。令:
 ,
, ,则:
,则: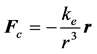
忽略电子与电子、电子与原子核之间的万有引力,设电子的质量为me,根据牛顿第二定律,建立如下矢量微分方程:
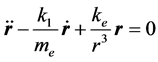 (1)
(1)
3.2. 电子受电磁场驱动运动方程
处于电磁场中原子,绕原子核旋转电子还要受到电磁场驱动,亦即在电磁场的变化磁场中受到洛伦兹力的驱动,在由变化磁场激发产生的涡旋电场中受到涡旋电场力的驱动(图6),这是外力驱动。因此,在(1)式方程右边加上这两个力的驱动,就得到绕原子核旋转电子受到库仑力驱动和电磁场驱动的运动方程:
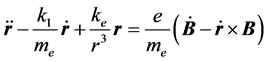 (2)
(2)
其中:b:电磁场之变化磁场的磁感应强度;根据法拉第电磁感应定律,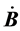 为涡旋电场强度;
为涡旋电场强度;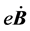 为涡旋电场力;
为涡旋电场力;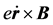 为洛伦兹力。(2)式是非齐次方程,其解的结构为齐次方程的通解加非齐次方程的特解。
为洛伦兹力。(2)式是非齐次方程,其解的结构为齐次方程的通解加非齐次方程的特解。
3.3. 受电磁场驱动运动方程求解
在《航天动力学基础》[12] 等书中,详细讨论了人造卫星与地球、地球与太阳一类两体运动方程的求解和轨道运动常数。参照这些书籍,求解核外电子受电磁场驱动运动方程(2)和运动常数在附录1中。其4个解如下:
(1) 电子受电磁场驱动吸收能量解
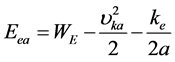 (3a)
(3a)
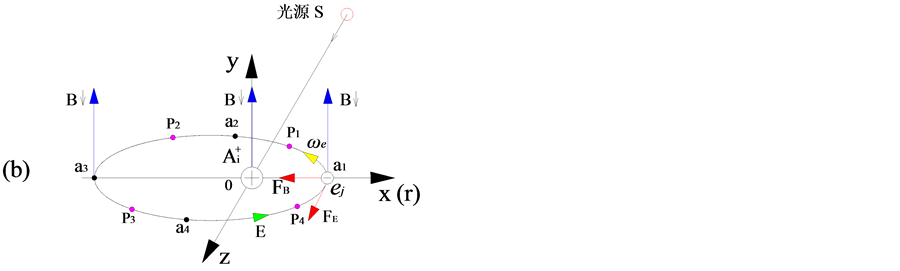
. the diagram of extranuclear subjected to lorentz force and vortex electric field force in the electromagnetic field; (a) the dimensional coordinate system from the source s to atomic ai; (b) elliptical orbit and schematic diagram of stress of the electronics ej
图6. 核外电子受电磁场涡旋电场力和洛伦兹力作用示意图;(a) 从光源s到原子ai的三维坐标系;(b) 电子ej椭圆轨道及受力示意图
 (3b)
(3b)
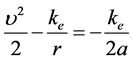 (3c)
(3c)
(2) 电子受电磁场驱动角动量解
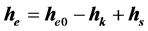 (4a)
(4a)
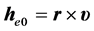 (4b)
(4b)
(3) 电子受电磁场驱动偏心率解
 (5)
(5)
(4) 电子受电磁场驱动运动轨迹解
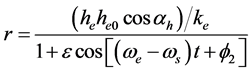 (6)
(6)
4. 方程解的应用——解释金属多峰值选择性光电效应
下面根据方程的解讨论产生光电效应的条件,然后重点解释本文开头提出的光的量子理论难以解释的金属多峰值选择性光电效应等问题。
4.1. 光电效应的判定
麦克斯韦在创立电磁场理论时明确指出:光是电磁波。光波的传播实质上是互激互生的变化磁场和涡旋电场的交替传播,是变化磁场激发产生涡旋电场,涡旋电场又激发产生变化磁场,是如此交替的持续传播。光电效应实质则是变化磁场和涡旋电场驱动绕核旋转电子脱离原子核、逸出金属表面的现象。那么,怎样判定电子已经逸出金属表面、产生光电效应呢?
根据电子受电磁场驱动运动轨迹解式(6),它是用极坐标表示的圆锥曲线,极点和焦点重合在原子核,长轴为极轴。偏心率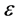 决定圆锥曲线的性质,二者有如下的关系:
决定圆锥曲线的性质,二者有如下的关系:
① 如果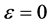 ,圆锥曲线为园,是椭圆的特例,表明电子绕核旋转轨迹是圆;
,圆锥曲线为园,是椭圆的特例,表明电子绕核旋转轨迹是圆;
② 如果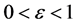 ,圆锥曲线为椭圆,表明电子绕核旋转轨迹是椭圆;
,圆锥曲线为椭圆,表明电子绕核旋转轨迹是椭圆;
③ 如果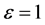 ,圆锥曲线为抛物线,表明电子的运动轨迹已经脱离椭圆,将沿着抛物线趋向无穷远,即
,圆锥曲线为抛物线,表明电子的运动轨迹已经脱离椭圆,将沿着抛物线趋向无穷远,即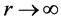 ;
;
④ 如果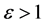 ,圆锥曲线为双曲线,表明电子的运动轨迹沿着双曲线趋向无穷远,即
,圆锥曲线为双曲线,表明电子的运动轨迹沿着双曲线趋向无穷远,即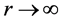 。
。
由此可以看出:当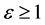 时,必有
时,必有 ,表明电子已经从绕核旋转的椭圆形轨道转移到抛物线、双曲线轨道,必将趋向无穷远,由此可以断定电子必将逸出金属表面,产生光电效应。这是产生光电效应的判据。
,表明电子已经从绕核旋转的椭圆形轨道转移到抛物线、双曲线轨道,必将趋向无穷远,由此可以断定电子必将逸出金属表面,产生光电效应。这是产生光电效应的判据。
诚然,在具体进行光电效应实验时,可根据实验环境确定一个r值,例如b,当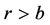 时,可以认定电子已经逸出,成为光电子。
时,可以认定电子已经逸出,成为光电子。
4.2. 产生光电效应的能量条件
怎样才能达到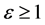 、
、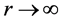 呢?根据电子受电磁场驱动偏心率解(5)式,当
呢?根据电子受电磁场驱动偏心率解(5)式,当 时,必有
时,必有 ,因此,
,因此, 是产生光电效应的能量条件。
是产生光电效应的能量条件。
根据电子受电磁场驱动受迫吸收能量解(3b),电子从电磁场中吸收的能量取决于涡旋电场的强度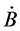 。根据电磁场理论[13] ,变化磁场可表达为
。根据电磁场理论[13] ,变化磁场可表达为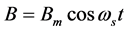 ,则:
,则:

以上式代入(2b)得到电子吸收的能量:
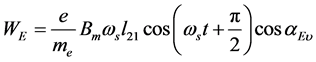 (7a)
(7a)
以(7a)式代入(3a),得:

要使能量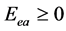 ,必须
,必须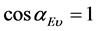 (即涡旋电场的方向与电子运动速度同向),于是有:
(即涡旋电场的方向与电子运动速度同向),于是有:
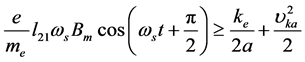 (7b)
(7b)
这是产生光电效应吸收能量的条件。上式左边是绕原子核旋转电子从电磁场中受迫吸收的能量,它与电磁场的频率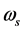 成正比,与电磁场的变化磁场强度
成正比,与电磁场的变化磁场强度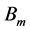 成正比,与电子被驱动移动的线积分
成正比,与电子被驱动移动的线积分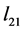 成正比,具有电磁场角频率的余弦函数周期性特性,对电磁场的频率没有限制。这种余弦函数的特性不同于线性方程,它不仅具有多峰值性,可以解释前面列举的多峰值选择性光电效应特性曲线,而且表达了吸收能量的积累时间只有电磁场频率的半个周期,或者说只有光波频率的半个周期,换句话说电子逸出的时间只能在这半个周期以内。上式右边是电子在原子核外具有的电位能和电子运动损耗的能量。
成正比,具有电磁场角频率的余弦函数周期性特性,对电磁场的频率没有限制。这种余弦函数的特性不同于线性方程,它不仅具有多峰值性,可以解释前面列举的多峰值选择性光电效应特性曲线,而且表达了吸收能量的积累时间只有电磁场频率的半个周期,或者说只有光波频率的半个周期,换句话说电子逸出的时间只能在这半个周期以内。上式右边是电子在原子核外具有的电位能和电子运动损耗的能量。
光电效应有4条实验规律,过去用波动学说解释这4条规律时,显示出尖锐矛盾有3条,即光电流与入射光频率的关系、遏止频率、产生光电效应的时间。过去认为:金属中的电子从入射光中吸收的能量,决定于光振动的振幅,即决定于光的强度,而与频率无关;电子吸收光的能量必须积累到一定的量值,入射光越弱,能量积累的时间就越长。基于这种认识产生了与实验规律的3大矛盾。显然,这种认识与(7b)式是不相符的,是没有理解光波电磁场的本质而产生的一种误解。依据(7b)式,3大矛盾也就迎刃而解了。
要达到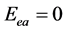 ,电子究竟吸收多大能量?根据:
,电子究竟吸收多大能量?根据:
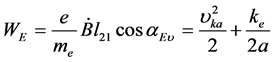
设阻力项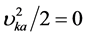 、设电子绕核旋转轨道半长轴a = 1 × 10−9 m(1纳米),则:
、设电子绕核旋转轨道半长轴a = 1 × 10−9 m(1纳米),则:
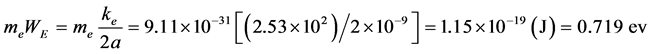
这一量值符合实际。
4.3. 产生光电效应的相位条件
根据电子受电磁场驱动运动轨迹解,在满足 、
、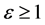 ,还不一定可以达到
,还不一定可以达到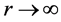 ,还必须满足相位条件,即(6)式分母为0:
,还必须满足相位条件,即(6)式分母为0:
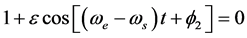
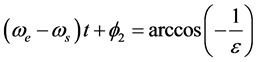 (8)
(8)
满足了(8)式,还必须满足(6)式分子不为0,即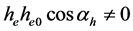 ,也就是电子绕核旋转的角动量不为0,只有在这时才能完全满足
,也就是电子绕核旋转的角动量不为0,只有在这时才能完全满足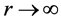 ,因此(8)式就是产生光电效应的相位角条件。
,因此(8)式就是产生光电效应的相位角条件。
4.4. 产生光电效应的暂态物理过程(电磁场1/4周期内)和电子的运动轨迹
光量子理论对于绕核旋转电子吸收光子能量产生光电效应的暂态物理过程,至今未见到论述的文献,仍然是当初爱因斯坦的设想:“只能整个地被吸收”。在本节,根据绕核旋转电子受电磁场驱动能量解和运动轨迹解,详细叙述电磁场两个作用力在1/4周期内驱动绕核旋转电子产生光电效应的暂态物理过程。1/4周期的时间有多长呢?以极远红外线的最低频率(波长750 μm)即周期最长的频率3.9972 × 1014 hz计算,1/4周期是2.50 × 10−15秒,这是本节描述暂态物理过程的时间长度。
根据绕核旋转电子受迫运动轨迹,过程可以分为以下五个阶段:椭圆形轨道上运动的初始状态、电磁场驱动穿越连续变化的能级、转移到抛物线轨道、转移到双曲线轨道、趋向无穷远。下面分别叙述电子的暂态运动过程。
(1) 椭圆形轨道上运动的初始状态
依据能量解(3c)式,电子在原子核的库仑引力作用下沿一条椭圆形轨道绕核旋转,电子的动能和电位能之和为负值、且与椭圆的半长轴成反比。在没有运动阻力损耗时,电子在核外椭圆轨道上稳定旋转,其轨道的半长轴保持为a。
要描述电子运动的暂态过程,必须选定观察点和在观察点处电子和电磁场的初始状态。现作如下选定:
观察点:在电子绕核稳定旋转的椭圆轨道上任选1点,今选择椭圆轨道上d1点。如图7a所示。
观察起始时间:电子逆时针旋转到d1点时,t = 0。
电子的初始状态:电子逆时针旋转,其动能和电位能之和小于0,即eea < 0,ε < 1。
电磁场的初始状态:电磁场的周期为ts,在t = 0之前,电磁场尚未传播到d1点;在t = 0时,电磁场刚好传播到d1点,恰好处于第3个1/4周期,此时电子受到电磁场的洛伦兹力fb和涡旋电场力fe如图7b所示。
(2) 电磁场驱动电子穿越连续变化的能级
在核外椭圆轨道上稳定旋转的电子,在d1点受到电磁场作用力fb的驱动,脱离原来的运动轨道向高能级运动,减少电子的电位能;同时又受到涡旋电场力fe的驱动,增加电子的动能;在t1 时刻,t1 < ts/4,电子的动能和电位能之和接近0,即eea ≈ 0,电子到达半长轴最大的临界椭圆形轨道上的d3点,临界椭圆轨道的半长轴为ac。在t1这段时间内,电子的运动轨迹从d1点经过d2点,到达d3点,从半长轴ab轨道运动到ac轨道,其间穿过一系列连续变化的椭圆形轨道,也就是穿越了一系列连续变化的能级(图8)。
(3) 转移到抛物线轨道
在t2时刻,t1 < t2
s/4,电子的动能和电位能之和e
ea = 0,ε = 1,电子从临界椭圆轨道转移到抛物线轨道。
(4) 转移到双曲线轨道
在t4时刻,t3 < t4 < ts/4,电子的动能和电位能之和eea > 0,ε > 1,此时,满足光电效应的相位条件:
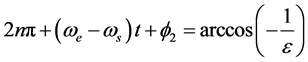
电子沿着双曲线轨道趋向无穷远,产生光电效应,绕核旋转电子变成了光电子。
4.5. 解释金属多峰值选择性光电效应
4.5.1. 吸收能量最少的轨道——轨道选择性
根据(7b)式产生光电效应的能量条件,当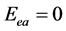 时,即:
时,即:
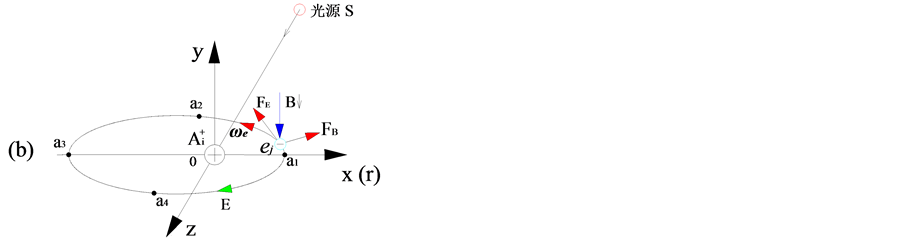
. the diagram of extranuclear subjected to two force at t = 0 in the electromagnetic field; (a) the schematic curve of changing magnetic field at d1; (b) the diagram of electronic subjected to fb and fe in the electromagnetic field at d1
图7. 绕核旋转电子在t = 0时运动位置及受电磁场两作用力示意图;(a) d1点变化磁场的变化曲线示意图;(b)电子在d1点受到电磁场的作用力fb和fe示意图

. the diagram of the electron driven by the electromagnetic field to endless distance when eea ≥ 0
图8. eea ≥ 0时电子被电磁场驱动转移到抛物线、双曲线轨道到达无穷远处示意图
 (7c)
(7c)
今设运动阻力损耗项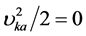 ,则
,则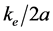 为常数。要使吸收的能量最少,只有a最大,也就是在原子核外最大半长轴amax的椭圆形轨道,是产生光电效应吸收能量最少的轨道。而最小半长轴amin吸收的能量最多。这说明光电效应具有轨道选择性,从而也可以说明原子核外不同的壳层轨道具有不同的逸出功。
为常数。要使吸收的能量最少,只有a最大,也就是在原子核外最大半长轴amax的椭圆形轨道,是产生光电效应吸收能量最少的轨道。而最小半长轴amin吸收的能量最多。这说明光电效应具有轨道选择性,从而也可以说明原子核外不同的壳层轨道具有不同的逸出功。
4.5.2. 产生光电效应的电磁场角频率——频率选择性
在满足了能量条件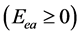 和角动量条件
和角动量条件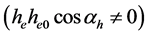 下,对于任一时刻t1,存在
下,对于任一时刻t1,存在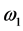 可以满足相位条件,即:
可以满足相位条件,即:
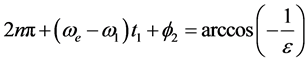
根据电子受电磁场驱动运动轨迹式(6),以轨迹r为纵坐标,以角频率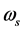 为横坐标,当
为横坐标,当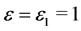 时,画出
时,画出 曲线图如9。图中当
曲线图如9。图中当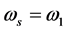 时,
时,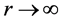 ,
,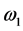 为轨迹位移最大的电磁场角频率;而当
为轨迹位移最大的电磁场角频率;而当 或者
或者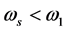 ,r都呈下降趋势。
,r都呈下降趋势。
在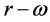 曲线图9中以核外最大半长轴
曲线图9中以核外最大半长轴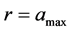 的直线,与曲线相交于两点d1与d2,与这两点对应的角频率为
的直线,与曲线相交于两点d1与d2,与这两点对应的角频率为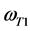 和
和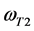 ,当角频率
,当角频率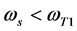 和
和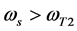 ,电子的轨迹
,电子的轨迹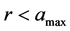 ,这表明电子都在绕核运动,并未摆脱原子核的束缚,当然不能产生光电效应。因此,在任一时刻t1,
,这表明电子都在绕核运动,并未摆脱原子核的束缚,当然不能产生光电效应。因此,在任一时刻t1,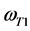 称为选择性光电效应的低端截止角频率,而
称为选择性光电效应的低端截止角频率,而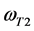 称为选择性光电效应的高端截止角频率,在
称为选择性光电效应的高端截止角频率,在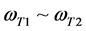 之间表现出具有频率选择性光电效应特性。
之间表现出具有频率选择性光电效应特性。
4.5.3. 产生光电效应的角频率群——频率多峰值选择性
在图9中已经说明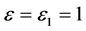 时,
时, 具有选择性光电效应特性的角频率,根据三角函数倍角关系式,当
具有选择性光电效应特性的角频率,根据三角函数倍角关系式,当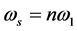 (n为正整数)时,
(n为正整数)时, 可以化为含有
可以化为含有 的频率成分,因此,
的频率成分,因此,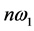 是产生光电效应的角频率群,在图9中可以进一步画出多峰曲线族(图10)。
是产生光电效应的角频率群,在图9中可以进一步画出多峰曲线族(图10)。
同样, (n为正整数)时,
(n为正整数)时,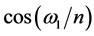 可以化为含有
可以化为含有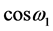 的频率成分,因此,
的频率成分,因此,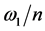 也是产生光电效应的角频率群。
也是产生光电效应的角频率群。
根据以上的叙述,说明金属的光电效应特性与频率不是线性关系,而是多峰值选择性曲线关系,这就很容易理解本文前面列举的金属多峰值选择性光电效应曲线的实例。
4.5.4. 任一频率不同时间点——时间多峰值选择性
在图9中,(ωs = ω1),在t1时刻,电子的受迫运动轨迹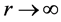 ,如果t1时刻不在余弦函数的峰值点,那么,在这一周期中还应该存在另一时刻t2,可以满足相位条件 (8)式,即:
,如果t1时刻不在余弦函数的峰值点,那么,在这一周期中还应该存在另一时刻t2,可以满足相位条件 (8)式,即:
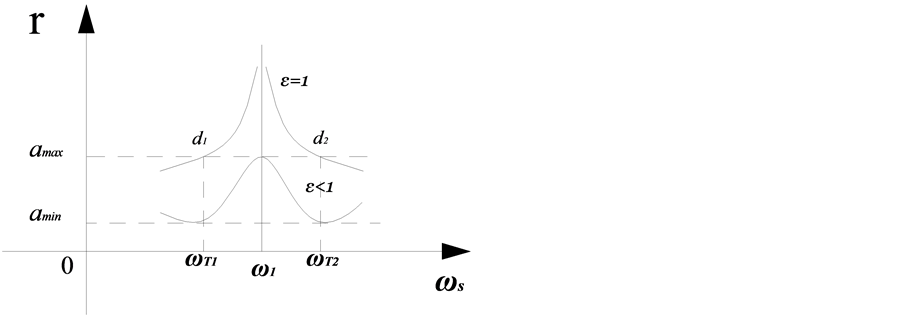
. selective spectral photoemission curves at any time
图9. 在任一时刻t1的选择性光电效应曲线

. multiple peaks selective photoemission curves and the trajectories of the electron about frequency at any time
图10. 在任一时刻t1电子运动轨迹与频率的多峰值特性曲线

. multiple peaks selective photoemission curves and the trajectories of the electron about time at any electromagnetic field frequency
图11. 对于电磁场任一频率电子运动轨迹与时间的多峰值特性曲线
条件。设(ωe-ω1)的周期为t,n为正整数,则:

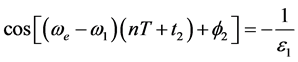
由此可知:在图11中还可以画出2n个多峰值选择性光电效应特性曲线。
在图11中,如果amax
b,表明电子已经逸出,产生了外光电效应。因此,电子的运动轨迹r在b~∞ 范围内是产生光电效应的轨迹条件。根据以上的叙述,说明金属的光电效应特性不仅与频率不是线性关系,而且与时间也不是线性关系,而是具有多峰值选择性曲线关系。
4.6. 光电效应γ截止限
γ截止限可以通过物质之磁导率μ来求证。因bm = μhm,以此代入(7a)式,得
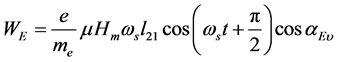 (9)
(9)
电磁场之涡旋电场力驱动电子所作的功we与物质之磁导率μ成正比的,而磁导率μ是频率的函数,随着频率的升高将趋于0。严密等编著的《磁学基础与磁性材料》[14] 一书在“磁谱与截止频率ft”一节中讨论了磁导率μ在交变磁场中随频率变化的关系曲线。书中指出:磁导率μ′随频率的增大而减小,磁滞损耗μ″随频率的增大而增大。μ′和μ″随交变磁场频率的变化曲线如图12所示。
在频率高端,μ趋于0,we亦趋于0,电子不能从电磁场中获得能量,也就不能产生光电效应。因此,光电效应出现了γ截止限。而用量子理论是很难解释它的。
4.7. 光电效应没有红限
在前面讨论光电效应的能量条件和相位条件所得出的表达式中,对电磁场的频率不存在限制,这是光电效应无红限频率的理论依据。
从图10中也可以看出无红限频率限制,相邻两条峰值选择性光电效应曲线的交点落入原子最大半径amax与原子核外最小半径amin之间,处于交点与最大半径之间的区域内的运动电子,受电磁场驱动吸收能量后,都可以从椭圆形轨道转移到抛物线轨道,产生光电效应。
过去物理实验测出的红限频率,也许是测量仪器的精度所限。根据粗算,如果产生1微安的光电流,则需要电磁场驱动每秒产生6.2415 × 1012个光电子。那么,电磁场的频率必须大于6.2415 × 1012 mhz

. magnetic spectrum curve and cutoff frequency ft
图12. 磁谱曲线和截止频率ft
才有可能,这正是红外的频率范围。而光电流小于1微安,测量仪器无法测出,在当时的条件下,也许认为不存在光电效应了。现在,如果采用测量光电子数量的仪器,一定能测出比红限频率低的频率仍能产生光电效应的真实情况。
1968年,teich 和wolga用gaas激光器发射的hν为1.48 ev的光子照射逸出功为2.3 ev的钠时,仍能产生光电效应[15] ,这是无红限一例,也是光量子学说是难以解释的。
4.8. 物质世界真空不空——存在热辐射电磁场激发逸出的运动电子
地球上的真空需要有容器,宇宙中的真空边缘存在稀薄气体,这真空容器以及稀薄气体周围始终存在光或者热辐射。按照麦克斯韦的电磁场理论,光和热辐射是电磁波,在电磁波所到之处存在电磁场。因此,真空容器以及稀薄气体中绕原子核旋转电子始终受到热辐射电磁场的驱动,只要满足下面条件,就能激发逸出电子:
(1) 能量条件
电子受电磁场驱动获得能量,使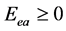 ,则
,则 ,电子就具备了激发逸出的能量条件。
,电子就具备了激发逸出的能量条件。
对于热辐射电磁场,其振幅很小。根据电磁波的叠加原理,如果有n个原子热辐射同频率、同相位角的电磁波,则合成波的变化磁场强度是单一波的n倍,因此低频电磁场的振幅条件也是容易满足的。
(2) 相位条件
具备能量条件后,且电子的角动量不为0,只要满足下式相位条件:

绕核转动电子的运动轨迹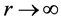 ,电子必然摆脱核的束缚,逸出核外,成为真空中的运动电子,这可称为电子隧穿。
,电子必然摆脱核的束缚,逸出核外,成为真空中的运动电子,这可称为电子隧穿。
由此可知,只要真空周围有光存在,有热辐射存在,也就是只要有电磁场存在,真空永远不空,真空中存在物质,存在热辐射电磁场激发逸出的运动电子,这为电磁场在真空中传播提供了物质依据。诚然,这还有待实验证实,这仅仅是时间早晚问题。
4.9. 产生光电效应的时间
由变化磁场激发产生的涡旋电场是时变场,在电磁场的ts/2内,其力的方向不变,在下一个ts/2,其力要改变方向。因此,在前一个ts/2时间内,涡旋电场力驱动电子吸收能量;在后一个ts/2时间内,涡旋电场力成为电子运动的阻力。要使电子受驱吸收能量,其最长时间不能超过ts/2,这就是吸收能量的最长时间。
由于电子在变化磁场中要受到洛伦兹力的驱动作用,在电磁场的一个周期中,洛伦兹力要改变一次方向,这就是说在电磁场的半个周期内,洛伦兹力为向心力,另半个周期为离心力。只有离心力的半个周期才能驱动电子脱离原子核,产生光电效应。又由于涡旋电场的相位滞后变化磁场ts/4,因此,只有在ts/4的时间内,才会出现洛伦兹力为离心力、涡旋电场驱动电子加速而使电子获得能量,从而产生光电效应。由此可知,产生光电效应的最长时间不超过电磁场的ts/4 (图13)。
电磁场的频率越高,其周期越短;频率越低,周期最长。在此以红外线的最低频率——极远红外线的最低端频率计算,该频率周期最长,吸收能量的时间最长,产生光电效应的时间也最长。极远红外线最低端波长为750 μm,频率为 3.9972ⅹ1014 hz 。 以此频率计算得到产生光电效应的最长时间:

. the maximum time that one photon energy is absorbed into the electron; (a) changing magnetic curve: b = bmcosωst (b) vortex electric field curve: e = −emsinωst
图13. 电子吸收一个光子能量的最长时间ts/4示意图;(a)变化磁场曲线:b = bmcosωst ;(b) 涡旋电场曲线:e = -emsinωst
5. 总结
100多年来,世界物理学界一直认为:电磁场、电动力学和牛顿力学这些经典理论在光电效应等粒子性物理现象面前失去了光彩。本文的面世,标志着这种观点已经成为历史,经典理论不仅能解释这些物理现象,而且能解释光量子理论难以解释的金属多峰值选择性光电效应。
真空中究竟存不存在物质?这个几百年来物理学界始终争论不休的论题,本文从理论上给出了肯定的答案:存在光或者热辐射电磁场驱动激发逸出的运动电子。虽然尚待实验证实,这只是时间早晚问题。真空中存在运动电子为电磁场在真空中传播提供了物质依据。
附录1
1. 核外电子受电磁场两力驱动微分方程的建立
先建立核外电子和原子核之间库仑力运动方程,再建立电子受电磁场涡旋电场力和洛伦兹力两外力驱动的微分方程。
1.1. 核外电子和原子核之间库仑力运动方程
1.1.1. 电子所受库仑力合力
核电荷数为z的物质m,其表面任意一个原子ai的核外应有z个电子,选择其中任意一个电子ej,分析其受力状况。它应受到如下这些力的作用:本原子核的库仑引力和万有引力、本原子核外其他电子的库仑斥力和万有引力、邻近原子核的库仑引力和万有引力、邻近原子核外电子的库仑斥力和万有引力、电子绕核旋转运动的阻力等。为使研究简单化,抓住主要的库仑力合力和电子运动阻力的作用,忽略次要的万有引力的作用。
研究电子ej受到的库仑力合力的大小,先研究在它的运动轨道上任意一点的电场强度en(本文中以黑体字母表示矢量)。
(1) 作静电场高斯第一闭区域
在某一极短极短的瞬间(如10−30秒,在此时间内高斯闭区域内电荷量不会因电子运动而发生变化),以ai原子核的中心为球心,以在轨道上运动的电子ej与核中心的连线(矢径)rj为半径作高斯球面(见图14),此球面为高斯第一闭区域,使区域内不包含电子ej,但包含原子核(核内含z个质子及中子等)、以及核外(j − 1)个电子,由于电子受力为有心力,其绕核旋转轨道为椭圆轨道,球内有可能多于(j-1)个电子,也可能少于(j − 1)个电子,暂以(j − 1)个电子考虑,若电子电荷量的绝对值为e (以下全文同),球内电荷的代数和为(z – j 1)e,其中(z > j ),根据高斯定理,则穿出球面的电场强度通量ψe1:

其中:e1为球内电荷在球面形成的电场强度,s为球的表面积,ε0为真空介电常量,r/r为单位矢径,在此表示电场强度通量的方向。
(2) 作静电场高斯第二闭区域
在上述作球面的同一瞬间,以ai原子核的中心为球心,以电子ej与核中心连线(矢径)rj为半径作内球面,使球内包含了电子ej,还包含了原子核、以及核外的(j − 1)个电子;同时,又以ai原子核的中心为球心,以电位为0(电场强度通量为0)的无穷远处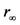 为半径作外球面(见图15),由于电场线终止于无穷远,则在无穷远外球面上无电场线进出,其电场强度为0,在内外两球面之间的闭区域内(高斯第二闭区域),包含了ai原子核外的(z − j)个电子(无论高斯第一闭区域内多于(j − 1)个电子,还是少于(j − 1)个电子,高斯第一和第二闭区域内电子总数应为(z − 1)个)、与ai原子邻近的原子及m的所有原子、以及m周围及无穷远以内的其他一切物质的所有原子,由于其内所有原子的质子和电子数量相等,显电中性,因此,内外球面之间的闭区域内,电荷的代数和为
为半径作外球面(见图15),由于电场线终止于无穷远,则在无穷远外球面上无电场线进出,其电场强度为0,在内外两球面之间的闭区域内(高斯第二闭区域),包含了ai原子核外的(z − j)个电子(无论高斯第一闭区域内多于(j − 1)个电子,还是少于(j − 1)个电子,高斯第一和第二闭区域内电子总数应为(z − 1)个)、与ai原子邻近的原子及m的所有原子、以及m周围及无穷远以内的其他一切物质的所有原子,由于其内所有原子的质子和电子数量相等,显电中性,因此,内外球面之间的闭区域内,电荷的代数和为
 ,根据高斯定理,则穿出内球面的电场强度通量ψe2:
,根据高斯定理,则穿出内球面的电场强度通量ψe2:

. the diagram of the sphere with rj radius applying gauss theorem
图14. 以rj作球面应用高斯定理示意图

. the diagram of the sphere with rj and 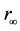 radius applying gauss theorem
radius applying gauss theorem
图15. 以内rj和外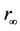 作球面应用高斯定理示意图
作球面应用高斯定理示意图
则电子ej旋转轨道上的ψe和en:
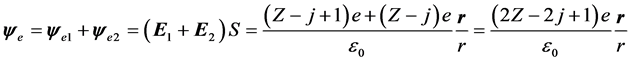
由于电子在核外空间区域不一定均匀分布,因而电场强度在高斯曲面上并非处处相等,为便于分析,取电场强度的平均值,因此,
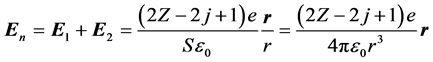
这是物质m内所有原子核以及所有核外电子(除ej外)在位于电子ej点的总电场强度,电场强度的方向为垂直于高斯球面的法线方向,电子ej所受到的库仑力的合力就是电场力fc,其大小为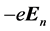 ,fc方向指向原子核,是有心力。
,fc方向指向原子核,是有心力。
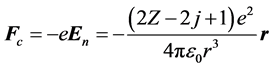 (1a)
(1a)
设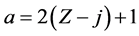 ,则:
,则:
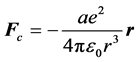 (1)
(1)
根据(1a)式可以得出1个重要结果:原子系统中任一电子在原子核外所受到的库仑力的合力fc与电子所处的壳层轨道有关,不同的壳层具有不同的库仑合力。
当j=1时,即ej为最内层电子时,fc为:
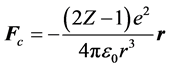 (1b)
(1b)
当j = z时,即ej为最外层电子时,fc为:
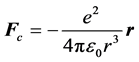 (1c)
(1c)
本文重点研究关联电子以(1)式为动力的运动规律。那么,电子对原子核的吸引力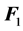 :
:
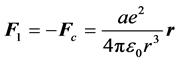 (1d)
(1d)
1.1.2. 建立库仑力运动方程
设原子核的质量为m1、电子的质量为me,在m内任取1点o作惯性参考点,o到m1和me的距离矢量为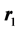 和
和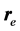 ,m1到me的相对距离矢量为r,则
,m1到me的相对距离矢量为r,则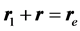 (图16)。
(图16)。
忽略电子与电子、电子与原子核之间的万有引力,根据牛顿第二定律:
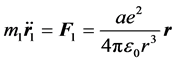
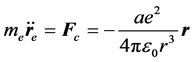
将上面两式相减,并引用矢量关系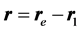 ,可得相对运动方程:
,可得相对运动方程:

由于质子、中子的质量是电子质量的1840倍,原子核的质量则远远大于电子的质量,即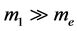 ,则:
,则:

因此,描述电子相对原子核的库仑引力运动方程为:
 (2)
(2)
考虑电子在绕核旋转运动中的阻力或能量损耗,该力与运动速度成正比,设阻力系数为k1,则该力为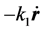 。令:
。令:
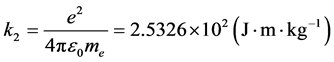 ,
,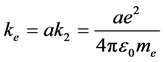 ,则:
,则: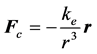
根据牛顿第二定律,建立如下矢量微分方程:
 (3)
(3)
1.1.3. 电子受电磁场驱动运动方程
处于电磁场中原子系统,绕原子核旋转电子还要受到电磁场驱动,亦即在电磁场的变化磁场中受到洛伦兹力fb的驱动,在由变化磁场激发产生的涡旋电场中受到涡旋电场力fe的驱动(图17),这是外力驱动。因此,在(3)式方程右边加上fb和fe的驱动,就得到绕原子核旋转电子受到库仑力驱动和电磁场驱动的运动方程:
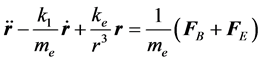
因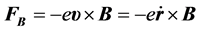 、
、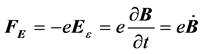 (e为电子电荷量的绝对值),故:
(e为电子电荷量的绝对值),故:
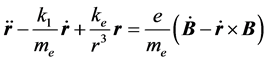 (4)
(4)
(4)式是非齐次方程,其解的结构为齐次方程的通解加非齐次方程的特解。
因阻力矢量表达式以及fb和fe的矢量表达式不可积,如果将上式化为以直角坐标表示的标量方程,则变成3个方程求解,比较麻烦。本文弃烦求简,将其变换为可积的矢量表达形式,根据牛顿第二定律,令:
图16. 电子和原子核间两粒子惯性参考系

. the diagram of extranuclear subjected to lorentz force and vortex electric field force in the electromagnetic field; (a) the dimensional coordinate system from the source s to atomic ai; (b) elliptical orbit and schematic diagram of stress of the electronics ej
图17. 电子和原子核间两粒子惯性参考系; (a) 从光源s到原子ai的三维坐标系;(b) 电子ej椭圆轨道及受力示意图
(5)式是(4)式的等效变换,仅仅是换了一种表达符号。
2. 受电磁场驱动运动方程的求解
在《航天动力学基础》[12] 等书中,详细讨论了人造卫星与地球、地球与太阳一类两体运动方程的求解和轨道运动常数。下面参照这些书籍,求解核外电子受电磁场驱动运动方程(5)和运动常数。
2.1. 能量解
用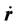 与方程(5)式作点积,得到:
与方程(5)式作点积,得到:
 (6)
(6)
先求齐次方程的通解:

由于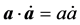 ,
,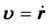 ,
,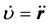 ,故:
,故:
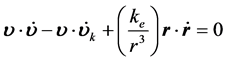
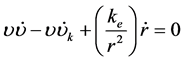
又由于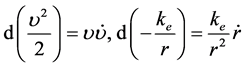 ,设:
,设: ,得:
,得:

两边积分,得:
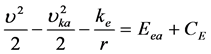 (7)
(7)
式中各项: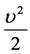 ——绕核转动电子所具有的单位质量的动能,或称电子的比动能;
——绕核转动电子所具有的单位质量的动能,或称电子的比动能;
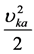 ——电子运动损耗的能量,损耗等于比动能时电子落入核中;
——电子运动损耗的能量,损耗等于比动能时电子落入核中;
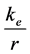 ——绕核转动电子所具有的电位能;
——绕核转动电子所具有的电位能;
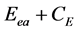 ——电子的比动能、电位能和损耗的能量之和,是电子的总能量,是常数,它表示电子在核外轨道上运动的总能量守恒。其中
——电子的比动能、电位能和损耗的能量之和,是电子的总能量,是常数,它表示电子在核外轨道上运动的总能量守恒。其中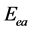 是积分原函数,
是积分原函数, 是积分任意常数,由初始条件确定。由于二者都是常数,可将其合并为一个
是积分任意常数,由初始条件确定。由于二者都是常数,可将其合并为一个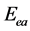 。因此总能量为:
。因此总能量为:
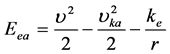 (8)
(8)
式(7)揭示了电子绕核旋转的动能、位能和损耗能量的关系,速度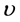 与r的反比关系。
与r的反比关系。
下面采用常数变易法求非齐次方程的特解。对式(7)求导代入(6)式,得到:

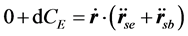
因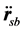 与
与 垂直,其点积为0,即
垂直,其点积为0,即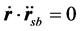 。这说明电子在电磁场中受到的洛伦兹力只改变运动方向,不改变电子的能量,对电子的能量贡献为0。故:
。这说明电子在电磁场中受到的洛伦兹力只改变运动方向,不改变电子的能量,对电子的能量贡献为0。故:
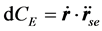
又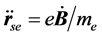 ,
,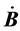 与
与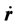 共线,其夹角
共线,其夹角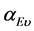 或为0,或为
或为0,或为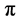 ,因此:
,因此:
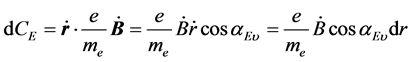
两边积分,设涡旋电场力驱动电子移动的轨迹区域为l,其线积分即移动轨迹的弧长为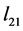 ,得到:
,得到:
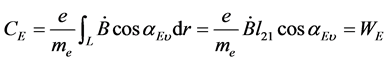 (9)
(9)
(9)式是电磁场驱动方程的特解,表示绕原子核旋转电子的单位质量从电磁场之涡旋电场中受驱动吸收的能量。由于涡旋电场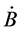 是时变量,
是时变量, 也是时变量。如果
也是时变量。如果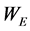 为正值,表示涡旋电场力驱动电子作加速运动;如果
为正值,表示涡旋电场力驱动电子作加速运动;如果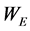 为负值,表示涡旋电场力驱动电子作减速运动,成为电子运动的阻力。
为负值,表示涡旋电场力驱动电子作减速运动,成为电子运动的阻力。
将齐次方程的通解和非齐次方程的特解相加,构成绕核旋转电子受电磁场fb和fe驱动方程的通解,是方程的能量解。
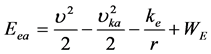 (10a)
(10a)
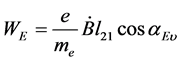 (10b)
(10b)
由(10b)式可知,电子在电磁场中受迫吸收的能量是连续变化的,非“跃迁”式变化的。由此可以解释电子吸收光子能量“整个地被吸收”、“部分吸收”、“双光子吸收”、“多光子吸收”等等,而且可以作图表达电子从电磁场吸收能量的过程,在电磁场的半个周期,电子吸收能量,另半个周期电子释放能量。
2.2. 轨道角动量解
用r与方程(5)式作叉积,得到:
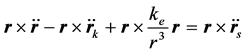 (11)
(11)
先求齐次方程的通解:

按矢量运算规则: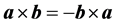 ,得:
,得:
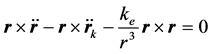
因 ,则有:
,则有:

因:
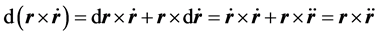
故:
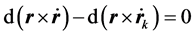
两边积分:

这里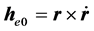 ,表示库仑力产生的角动量;
,表示库仑力产生的角动量;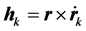 ,表示运动阻力产生的角动量。上式也可以表示为:
,表示运动阻力产生的角动量。上式也可以表示为:
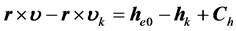 (12)
(12)
当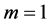 时,动量
时,动量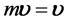 ,表示单位质量的动量;
,表示单位质量的动量;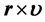 表示单位质量动量矩、或单位质量角动量。
表示单位质量动量矩、或单位质量角动量。 为积分任意常矢量,由初始条件确定。由于上式右边都是常矢量,而且共线,可将
为积分任意常矢量,由初始条件确定。由于上式右边都是常矢量,而且共线,可将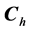 合并到
合并到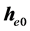 。
。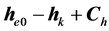 为常矢量,表示电子在核外轨道运动的角动量守恒。因此,总角动量为:
为常矢量,表示电子在核外轨道运动的角动量守恒。因此,总角动量为:
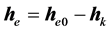 (13)
(13)
下面采用常数变易法求非齐次方程的特解:
对(12)求导代入(11)式,得到:
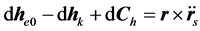
因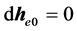 ,
,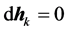 ,得
,得

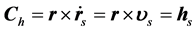 (14)
(14)
这里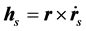 ,表示电磁场驱动力产生的角动量。
,表示电磁场驱动力产生的角动量。
将齐次方程的通解和非齐次方程的特解相加,构成方程(5)的轨道角动量解,即:
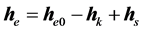 (15a)
(15a)
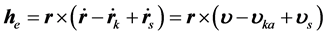 (15b)
(15b)
2.3. 轨道偏心率解
方程(5)与常矢量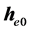 叉积,得到一个可积分的形式:
叉积,得到一个可积分的形式:
 (16)
(16)
先求齐次方程的通解:
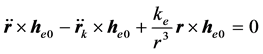
按矢量运算规则: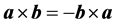 ,得:
,得:
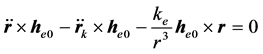
因:
又: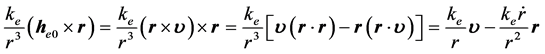
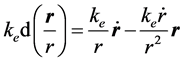
因此:
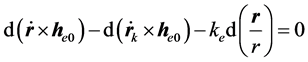
两边积分
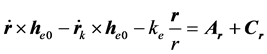 (17)
(17)
积分矢量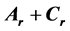 为常矢量,表示积分矢量的变化率守恒,
为常矢量,表示积分矢量的变化率守恒,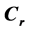 为积分任意常矢量,与
为积分任意常矢量,与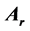 同向,可将其合并到
同向,可将其合并到 。
。
令: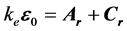 ,
,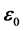 为偏心率矢量,它是由电子受到的库仑力和运动阻力产生的。因此得:
为偏心率矢量,它是由电子受到的库仑力和运动阻力产生的。因此得:
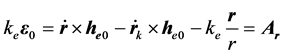 (18)
(18)
化简,以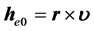 代入得:
代入得:
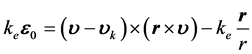
根据矢量运算规则得:
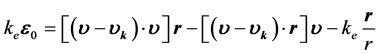
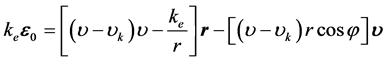 (19)
(19)
由此可知,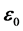 的导矢为0,其角速度与r相同,与r相差一个相位角,是园函数矢量。
的导矢为0,其角速度与r相同,与r相差一个相位角,是园函数矢量。
下面采用常数变易法求非齐次方程的特解,对(17)求导代入(16)式,得到:
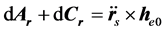
因 ,故
,故
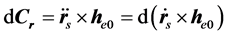
两边积分得特解:
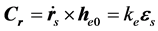 (20)
(20)
这里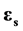 是由电磁场驱动力产生的。
是由电磁场驱动力产生的。
将齐次方程的通解和非齐次方程的特解相加,构成方程(5)的轨道偏心率解,即:
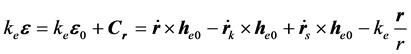 (21)
(21)
或者:
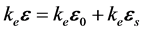 (22a)
(22a)
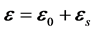 (22)
(22)
2.4. 轨迹方程解
2.4.1. 齐次方程解
以r点乘偏心率矢量(18)式两端得到标量方程:
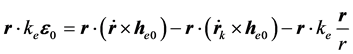
根据矢量运算规则: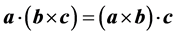 ,
,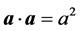 ;及前边
;及前边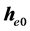 和
和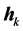 的定义:
的定义: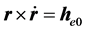 ,
,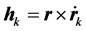 ,则:
,则:


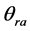 为矢径r与常矢量
为矢径r与常矢量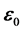 的夹角,它与极角
的夹角,它与极角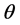 的关系为:
的关系为: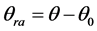 (图18),
(图18),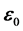 与极轴的夹角为
与极轴的夹角为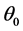 。解出r得到以极坐标表示的齐次方程的通解:
。解出r得到以极坐标表示的齐次方程的通解:
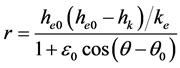 (23a)
(23a)
在无阻力即无损耗时,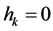 ,上式变为:
,上式变为:
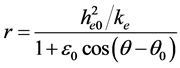 (23b)
(23b)
2.4.2. 非齐次方程的解
以r点乘偏心率矢量(20)式两端得到标量方程:
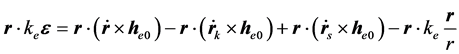
根据矢量运算规则: ,
,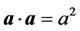 ;及前边
;及前边 、
、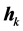 和的定义:
和的定义: ,
,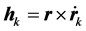 ,
,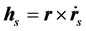 ,则:
,则:
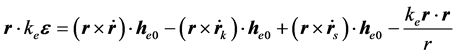

因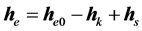 ,设
,设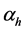 为
为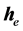 与
与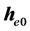 的夹角,
的夹角,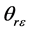 为r与
为r与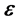 的夹角,则上式变为:
的夹角,则上式变为:
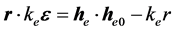
图18. 矢径r与常矢量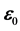 的夹角关系
的夹角关系
2.4.3. 解出
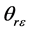 为r与偏心率矢量
为r与偏心率矢量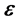 的夹角,下面对
的夹角,下面对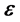 进行粗略分析。
进行粗略分析。
根据(22)式可知,这实际上是两个运动的合成问题,比较复杂,本文下面只讨论二者同轨道平面同旋转方向合成的简单问题。
设电子ej以角速度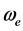 逆时针绕核旋转,在任意时刻t,其相位角
逆时针绕核旋转,在任意时刻t,其相位角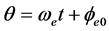 ,
,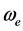 是电子绕核旋转的固有角速度或固有角频率,
是电子绕核旋转的固有角速度或固有角频率,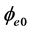 为电子绕核旋转的初相角。
为电子绕核旋转的初相角。
根据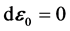 可知,
可知,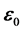 是园函数矢量,其大小不变,其旋转方向和角速度与电子ej相同,其相位角比电子ej滞后
是园函数矢量,其大小不变,其旋转方向和角速度与电子ej相同,其相位角比电子ej滞后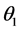 ,在任意时刻t,其相位角
,在任意时刻t,其相位角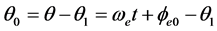 。
。
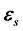 随电磁场的频率、振幅而变,设其旋转方向与电子ej相同,在电子绕核旋转的轨道平面上,为逆时针方向,其角速度为
随电磁场的频率、振幅而变,设其旋转方向与电子ej相同,在电子绕核旋转的轨道平面上,为逆时针方向,其角速度为 ,在任意时刻t,其相位角
,在任意时刻t,其相位角 ,其中
,其中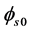 为电磁场的初相角。
为电磁场的初相角。
设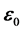 和
和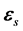 的合矢量
的合矢量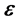 的角速度为
的角速度为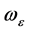 ,在任意时刻t,其相位角
,在任意时刻t,其相位角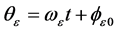 ,其中
,其中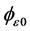 为合矢量
为合矢量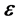 的初相角。
的初相角。
设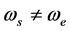 ,则在任意时刻t,
,则在任意时刻t,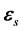 和
和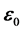 的相位角之差为(见图19):
的相位角之差为(见图19):


设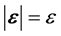 、
、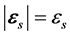 、
、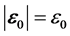 ,根据余弦定理,则
,根据余弦定理,则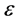 为:
为:
 (25)
(25)
根据正弦定理,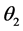 为:
为:
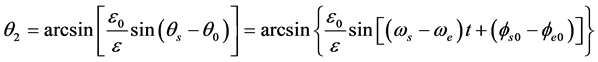 (26)
(26)
由图19可求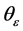 及
及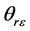 :
:

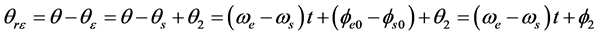
即:
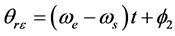 (27)
(27)
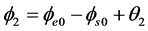 (27a)
(27a)
(27)式中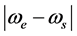 就是新的角速度,即新的角频率,是受驱偏心率矢量
就是新的角速度,即新的角频率,是受驱偏心率矢量 的角频率。当
的角频率。当 时,新的角频率是
时,新的角频率是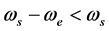 ;当
;当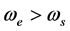 时,新的角频率是
时,新的角频率是 。
。
以(27)式代入(24)式,得以极坐标表示的非齐次方程的解,是绕原子核转动电子受电磁场驱动的受驱运动轨迹方程,是圆锥曲线一般方程:
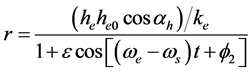 (28)
(28)
式(28)是用极坐标表示的圆锥曲线,极点和焦点重合在原子核,长轴为极轴。圆锥曲线的性质由偏心率决定:
① 当 ,圆锥曲线的轨道为园,园是椭圆的特例;
,圆锥曲线的轨道为园,园是椭圆的特例;
② 当 ,圆锥曲线的轨道为椭圆;
,圆锥曲线的轨道为椭圆;
③ 当 ,圆锥曲线的轨道为抛物线;
,圆锥曲线的轨道为抛物线;
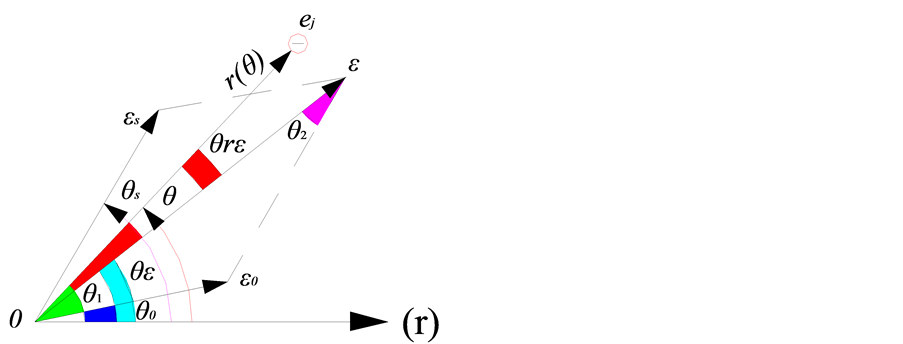
. the angle diagrams of the radius vector r and eccentricity vector 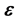
图19. 电子旋转矢径r与偏心率矢量的角度关系
④ 当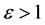 ,圆锥曲线的轨道为双曲线。
,圆锥曲线的轨道为双曲线。
2.5. 电子在圆锥曲线轨道上运动的能量
这里计算在无电磁场环境中,即没有电磁场驱动时,电子在圆锥曲线轨道上运动所具有的能量。由此,根据(23b)式以及圆锥曲线的特征,可得:
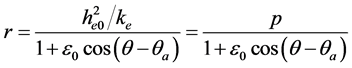 (23b1)
(23b1)
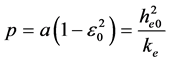
 (30)
(30)
其中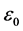 为偏心率、p为半正焦弦、a为半长轴。轨道与长轴的交点坐标rq
为偏心率、p为半正焦弦、a为半长轴。轨道与长轴的交点坐标rq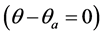 为:
为:
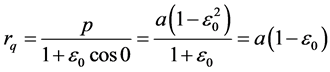
在交点rq上,矢径r与速度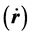
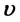 垂直,因此,
垂直,因此,
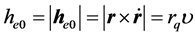
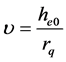
将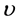 、
、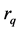 、
、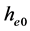 代入能量解(8)式,得:
代入能量解(8)式,得:
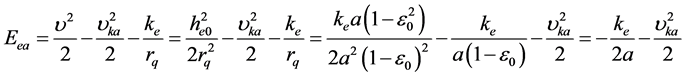
 (31)
(31)
上式表明:核外电子在绕核旋转轨道上运动的总能量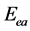 (电子的动能、损耗和电位能之和)为负值,其大小与绕核运动轨道的半长轴
(电子的动能、损耗和电位能之和)为负值,其大小与绕核运动轨道的半长轴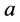 成反比,与原子核电荷数z成正比(因
成反比,与原子核电荷数z成正比(因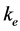 与原子核电荷数z成正比)。因此,能量解(10a)式可化为:
与原子核电荷数z成正比)。因此,能量解(10a)式可化为:
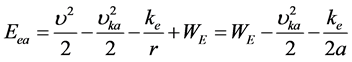 (32)
(32)
根据(31)式还可以得到一个重要结论:核外电子在绕核旋转轨道上运动,永远具有负能量,其能量只依库仑力的存在而存在,只依电荷的存在而存在,而与温度无关。无论在任何温度下,甚至在绝对0度(-273.13k)及其以下,只要原子核和电子的电荷存在,原子核和电子之间的库仑力就始终存在,电子与核之间库仑力运动方程(3)式始终成立,方程的能量解(8)式始终存在,电子所具有的负能量也就永远存在,该能量称之为0点能。
2.6. 偏心率与能量的关系
根据(30)式,得:
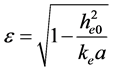 (33)
(33)
根据(31)式,设损耗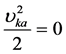 ,得:
,得:
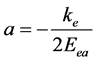
将上式代入(33)式,得偏心率与能量的关系式:
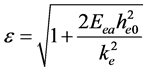 (34)
(34)
由此可以得出:
当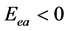 时,
时,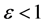 ,这是库仑力的贡献;
,这是库仑力的贡献;
当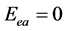 时,
时, ,因为电子在库仑力作用下,其能量永远为负值,电子只有在电磁场中吸收能量后,才能达到能量为0;
,因为电子在库仑力作用下,其能量永远为负值,电子只有在电磁场中吸收能量后,才能达到能量为0;
当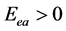 时,
时,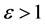 ,电子只有在电磁场中吸收能量后,才能达到能量大于0。
,电子只有在电磁场中吸收能量后,才能达到能量大于0。