1. 引言
基于三态开关单元(three-state switching cell)的传统两相交错并联dc/dc变换器可以增强功率等级,减小输入电流纹波,因此在不间断电源(ups)、功率因数校正等不需较大升压变比的场合得到了广泛应用。已将其列入电力电子拓扑的一个重要基本架构,国内外许多学者把这种基本架构作为主要组成部分,提出和研究了多种特点各异、适用于不同场合、满足于不同性能要求和用途的高性能电路拓扑 [1] - [22] 。其中如何提高三态开关交错并联dc/dc变换器的电压增益,已成为电力电子技术的重要研究内容之一。
与单相高增益dc/dc变换器相同,若分别把开关电容或耦合电感引入到输入、输出端并联的dc/dc变换器中,可以提高输出电压增益,但这两种方法各有优缺点。单独使用开关电容的交错并联dc/dc变换器 [6] [7] [8] ,可以降低开关管和二极管的电压应力,但其电压增益的进一步提高,通常依靠增加开关电容的级数来实现。每增加一级开关电容都包含多个二极管和电容元器件(至少一个二极管,一个电容),如果要实现较高的电压增益则往往需要很多的器件数量,而且电压增益是以整数倍增加,其调节电压增益的灵活性受到限制。另外,当开关管导通瞬间,通常会出现一个电容通过开关管直接对另一个电容充电的现象,此时电容相当于短路,所以过冲电流现象比较严重,实际使用时必须加以限制。如果将耦合电感应用到输入端交错并联的三态开关dc/dc变换器中 [9] [10] [11] [12] [13] ,不仅提高了变换器的输出电压增益,而且还增加了控制电压增益的灵活性,但耦合电感的漏感通常会引起开关电压尖峰,增大功率器件的电压应力等。将开关电容与耦合电感结合在一起 [1] [2] [3] [4] [5] ,可以发挥各自优点和相互弥补不足之处,有些文献也提出了一些电路拓扑 [14] - [22] ,但还需要进一步探索系统性构造方法及其规律。
本文从传统三态开关交错并联dc/dc变换器的基本结构出发,将耦合电感和二极管电容同时融合到传统的交错并联dc/dc变换器中,构造基于三态开关单元与双耦合电感的新型输入端交错并联高增益dc/dc变换器。当开关导通时,电源直接作用的是耦合电感一次绕组,将双耦合电感的一次绕组分别替代传统交错并联dc/dc变换器的两个分立电感,将耦合电感的二次绕组与其融合二极管电容的衍生结构分别看作两个独立的倍压单元,应用到双耦合电感输入端交错并联三态开关dc/dc变换器中,进一步提出了一种新型高增益非隔离型dc/dc变换器拓扑,对该变换器的工作原理及特性进行了分析,该变换器具有输入输出电压变换比高,开关器件的电压和电流应力低,输入电流纹波低等特点。
2. 新型dc/dc变换器
2.1. 拓扑结构
基于三态开关单元的高增益dc/dc变换器拓扑结构如图1所示。耦合电感可以用励磁电感、理想变压器、漏感来等效,等效电路如图2所示。其中l1、l2是两个耦合电感,lm1和lm2是励磁电感,lk1和
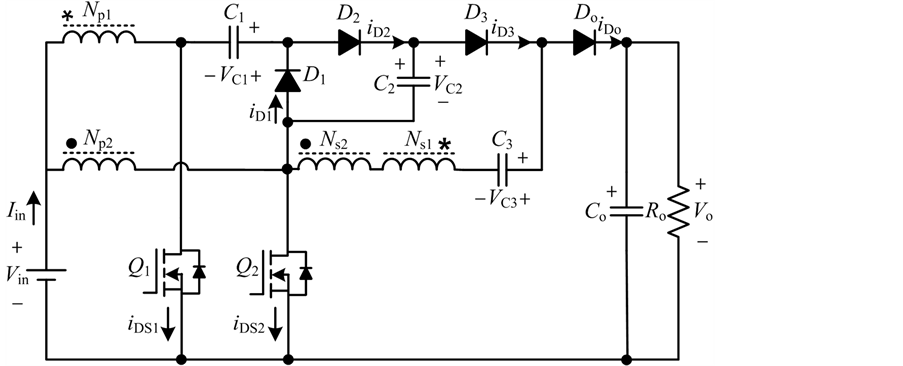
. circuit configuration of novel dc/dc converter
图1. 新型dc/dc变换器拓扑结构
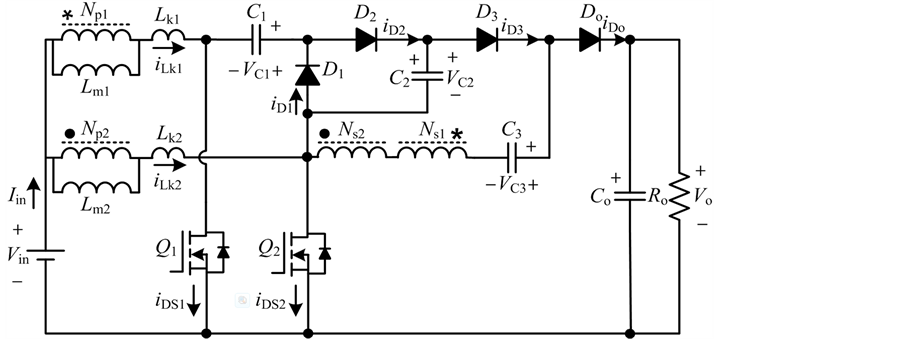
. equivalent circuit of novel dc/dc converter
图2. 新型dc/dc变换器等效电路
lk2是漏感,d1、d2、d3、do为续流二极管,c1为箝位电容,c2、c3为储能电容,co为输出滤波电容,q1、q2是两只主开关管,采用交错控制,它们的驱动信号相差180˚相角。
2.2. 工作原理分析
为了简化分析,假设:(1) 所有半导体功率器件均为理想器件;(2) 两个耦合电感的所有参数完全一致,lm1、lm2分别为原边激磁电感,且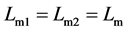 ;lk1、lk2分别为折算到原边的漏电感,且
;lk1、lk2分别为折算到原边的漏电感,且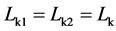 ,两个耦合电感原、副边绕组的匝比
,两个耦合电感原、副边绕组的匝比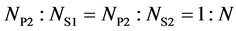 ;(3) 激磁电感的感值足够大,电路工作在连续状态。
;(3) 激磁电感的感值足够大,电路工作在连续状态。
一个工作周期内,电路共有8个工作模态。电路的主要波形如图3所示。稳定工作时,各模态下的等效电路如图4所示。
开关模态1[t0-t1]:如图4(a)所示,在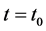 时刻,功率开关管q1和q2处于导通状态,二极管d1、d2和do关断;耦合电感副边绕组的漏感电流通过二极管d3向电容c3充电,且id3近似线性减小。同时两个耦合电感的二次绕组反向串联连接所产生的等效漏感之和对流过d3的拖尾电流具有限制作用,可以实现该二极管的零电流关断,进而有效减小二极管的反向恢复损耗。原边漏感电流ilk1快速增加,漏
时刻,功率开关管q1和q2处于导通状态,二极管d1、d2和do关断;耦合电感副边绕组的漏感电流通过二极管d3向电容c3充电,且id3近似线性减小。同时两个耦合电感的二次绕组反向串联连接所产生的等效漏感之和对流过d3的拖尾电流具有限制作用,可以实现该二极管的零电流关断,进而有效减小二极管的反向恢复损耗。原边漏感电流ilk1快速增加,漏
感电流ilk2以较快的速度线性减小。当漏感电流ilk1等于激磁电流ilm1时,该模态结束,此过程较短。
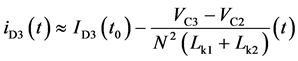 (1)
(1)
开关模态2[t1-t2]:如图4(b)所示,在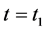 时刻,功率开关管q1、q2继续导通,所有二极管均关断。励磁电感lm1与lm2、漏感lk1与lk2在输入电压vin的作用下线性充电储能,其电流线性增加。由输出滤波电容co向负载提供能量。
时刻,功率开关管q1、q2继续导通,所有二极管均关断。励磁电感lm1与lm2、漏感lk1与lk2在输入电压vin的作用下线性充电储能,其电流线性增加。由输出滤波电容co向负载提供能量。

. typical waveforms of the proposed converter operated in ccm
图3. 工作于ccm模式的变换器关键工作波形
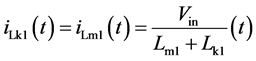 (2)
(2)
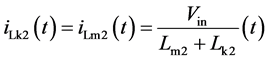 (3)
(3)
开关模态3[t2-t3]:如图4(c)所示,在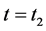 时刻,关断功率开关管q2,q1继续导通,二极管do导通,d1、d2和d3关断。输入电源继续对激磁电感lm1和漏感lk1充电,存储在磁化电感lm2中的能量通过耦合电感副边和二极管do向负载提供能量,电容c3向负载放电,同时存储于漏感lk2中的能量通过二极管d1和q1对电容c1充电。功率开关管q2的漏源极电压被二极管d1钳位在vc1,有效抑制了开关管的关断电压尖峰。另外由于耦合感的作用,限制了对电容c1充电电流的过冲现象。
时刻,关断功率开关管q2,q1继续导通,二极管do导通,d1、d2和d3关断。输入电源继续对激磁电感lm1和漏感lk1充电,存储在磁化电感lm2中的能量通过耦合电感副边和二极管do向负载提供能量,电容c3向负载放电,同时存储于漏感lk2中的能量通过二极管d1和q1对电容c1充电。功率开关管q2的漏源极电压被二极管d1钳位在vc1,有效抑制了开关管的关断电压尖峰。另外由于耦合感的作用,限制了对电容c1充电电流的过冲现象。
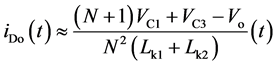 (4)
(4)
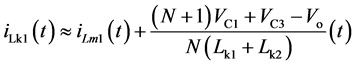 (5)
(5)
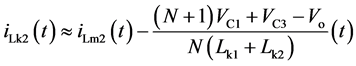 (6)
(6)
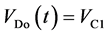 (7)
(7)
开关模态4[t3-t4]:如图4(d)所示,该模态中,功率开关管q1持续导通,q2持续关断。在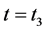 时,漏感lk2的能量已释放完毕,二极管d1自然关断,因此大大减小了该二极管反向恢复问题。励磁电感lm2所存储的能量仍然通过耦合电感的副边绕组和二极管do向负载传递能量,流过二极管do的电流近似线性下降。
时,漏感lk2的能量已释放完毕,二极管d1自然关断,因此大大减小了该二极管反向恢复问题。励磁电感lm2所存储的能量仍然通过耦合电感的副边绕组和二极管do向负载传递能量,流过二极管do的电流近似线性下降。
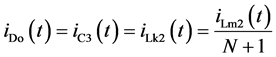 (8)
(8)
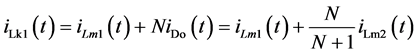 (9)
(9)
开关模态5[t4-t5]:如图4(e)所示,在 时刻,开通功率开关管q2,漏感电流ilk2快速上升,由于两个耦合电感副边绕组的串联效应,漏感电流ilk1近似线性下降。耦合电感的副边绕组仍然通过do向负载传输能量;当漏感电流ilk2等于激磁电流ilm2时,该模态结束,此过程较短。
时刻,开通功率开关管q2,漏感电流ilk2快速上升,由于两个耦合电感副边绕组的串联效应,漏感电流ilk1近似线性下降。耦合电感的副边绕组仍然通过do向负载传输能量;当漏感电流ilk2等于激磁电流ilm2时,该模态结束,此过程较短。
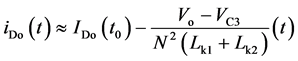 (10)
(10)
开关模态6[t5-t6]:如图4(f)所示,该模态中,两个功率开关管同时处于导通状态,和开关模态2的工作状态相同。
开关模态7[t6-t7]:如图4(g)所示,在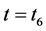 时刻,功率开关管q1关断,储存在漏感lk1中的能量通过开关管q2和二极管d2向电容c2充电,同时通过耦合电感副边绕组和二极管d3对电容c3充电。漏感电流ilk1近似线性下降,漏感电流ilk2在耦合电感副边绕组的串联效应下近似线性增加。功率开关管q1的漏源极电压被二极管d2钳位在(vc2-vc1)。
时刻,功率开关管q1关断,储存在漏感lk1中的能量通过开关管q2和二极管d2向电容c2充电,同时通过耦合电感副边绕组和二极管d3对电容c3充电。漏感电流ilk1近似线性下降,漏感电流ilk2在耦合电感副边绕组的串联效应下近似线性增加。功率开关管q1的漏源极电压被二极管d2钳位在(vc2-vc1)。
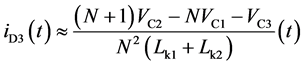 (11)
(11)
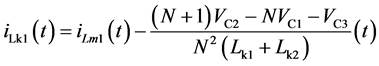 (12)
(12)
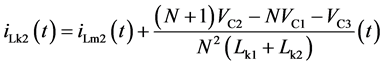 (13)
(13)
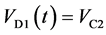 (14)
(14)
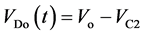 (15)
(15)
开关模态8[t7-t0’]:如图3(h)所示,在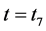 时刻,由于漏感电流ilk1逐渐减小到零,二极管d2自然关断。输入电压通过漏感lk2与,通过耦合电感副边绕组和二极管d3对电容c3充电。
时刻,由于漏感电流ilk1逐渐减小到零,二极管d2自然关断。输入电压通过漏感lk2与,通过耦合电感副边绕组和二极管d3对电容c3充电。
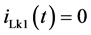 (16)
(16)
 (17)
(17)
 (18)
(18)
3. 稳态工作性能分析
3.1. 稳态电压增益
耦合电感的耦合系数k为 。
。
根据图4(b) 和图4(f)给出以下表达式:
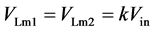 (19)
(19)
根据图4(c)给出以下表达式:
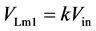 (20)
(20)
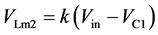 (21)
(21)
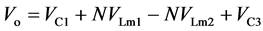 (22)
(22)
根据图4(g)给出以下表达式:
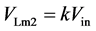 (23)
(23)
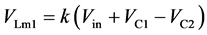 (24)
(24)
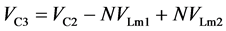 (25)
(25)
根据耦合电感的励磁电感lm1、lm2的伏秒平衡原理,可得到以下等式:
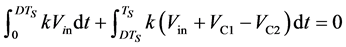 (26)
(26)
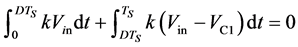 (27)
(27)
由式(25)、(26)、(27)得出:
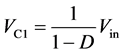 (28)
(28)
 (29)
(29)
 (30)
(30)
结合式(22)、(28)及(30),推出变换器输出电压表达式为:
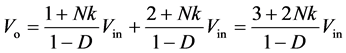 (31)
(31)
变换器电压增益表达式为:
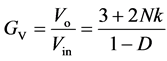 (32)
(32)
当k = 1时,该变换器电压增益表达式为:
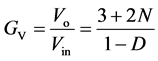 (33)
(33)
图5给出新型变换器与文献 [1] [2] 中变换器的电压增益与占空比之间的关系。从图5中可以看出,新型变换器与文献 [1] [2] 中变换器的电压增益随占空比增加而增加,但在相同占空比下,文中新型变换器的电压增益明显高于文献 [1] [2] 中变换器的电压增益。
图6给出输出电压增益与不同参数之间的关系。图6(a)给出在耦合电感的变比n = 2下,输出电压增益与占空比及耦合系数k之间的关系。从图6(a)中可以看出,在占空比相同时,耦合系数对电压增益的影响不大。图6(b)给出在耦合系数k=1下,输出电压增益与占空比及耦合电感的变比n之间的关系。从图6(b)中可以看出,在占空比相同时,输出电压增益随耦合电感变比增大而大幅度增大。
3.2. 电压应力
如果忽略电容电压的纹波以及耦合电感的漏感,结合模态分析可以计算出功率开关管q1、q2及二极管d1、d2、d3、do的最大电压应力分别为:
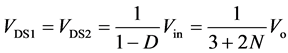 (34)
(34)
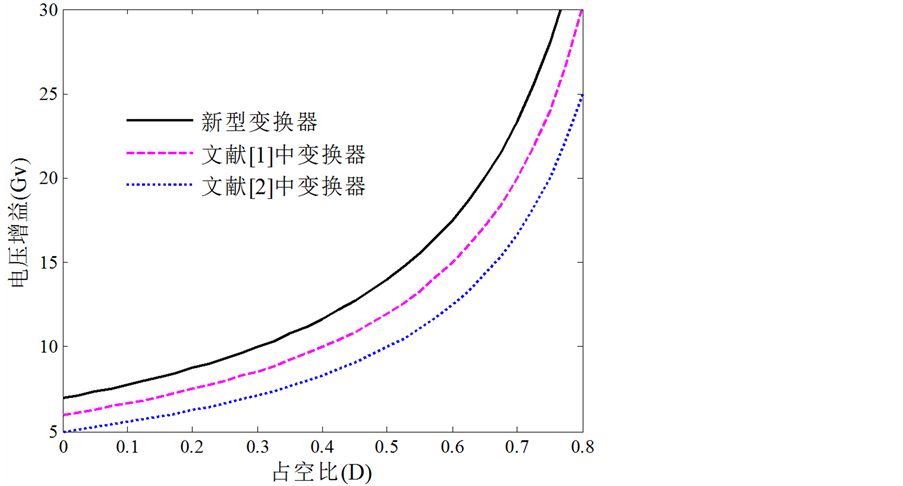
. voltage gain versus duty ratio of the proposed converter, the converters in [1] [2]
图5. 新型变换器及文献 [1] [2] 中变换器电压增益与占空比之间的关系
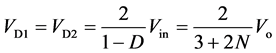 (35)
(35)
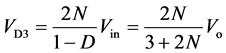 (36)
(36)
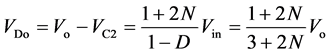 (37)
(37)
图7是功率器件的电压应力与耦合电感变比的关系,可以看出主开关管和二极管d1、d2的电压应力

 (a) 在n = 2下电压增益与占空比及耦合系数k之间的关系 (b) 在k = 1下电压增益与占空比及耦合电感变比n之间的关系
(a) 在n = 2下电压增益与占空比及耦合系数k之间的关系 (b) 在k = 1下电压增益与占空比及耦合电感变比n之间的关系
. voltage gain versus different parameters
图6. 电压增益与不同参数之间的关系
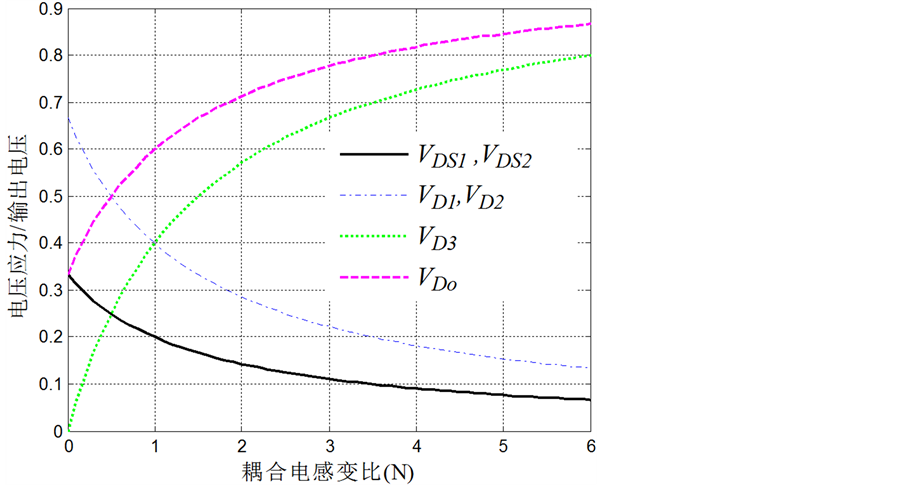
. voltage stresses on semiconductor components versus turns ratio n
图7. 变换器功率器件的电压应力
随着匝比的增加快速减小,当匝比为1时主开关的电压应力仅为输出电压的1/5,d1、d2、d3的电压应力低于输出电压的2/5。尽管二极管d3和do的电压应力随着匝比的增加呈上升趋势,但不会超过输出电压。
4. 仿真分析
为了验证理论分析的正确性,应用matlab软件对新型变换器进行仿真。仿真参数如下:输入电压vin = 10 v;输出电压vo = 100 v;输出功率po = 500 w;开关频率fs为20 khz,占空比d = 0.6;耦合电感耦合系数k = 0.98;耦合电感的自感l1 = l2 = 60 μh,因此耦合电感的互感lm = 58.9 μh。
图8给出了新型变换器的仿真波形,图8(a)中分别为总输入电流、两个耦合电感原边电流的仿真波形。可以看出,尽管每条输入支路的电流纹波较大,但通过交错并联控制,变换器的总输入电流纹波得到了大大减小,提高了变换器的性能;图8(b)中分别为开关管q的驱动波形及其对应的电压仿真波形,可以看出,当匝比为1时,开关管的电压应力近似等于输出电压vo的1/5;图8(c)中分别为二极管d1、d2、d3、do的电压仿真波形,当匝比为1时,二极管d1、d2、d3上的电压应力近似等于输出电压vo的
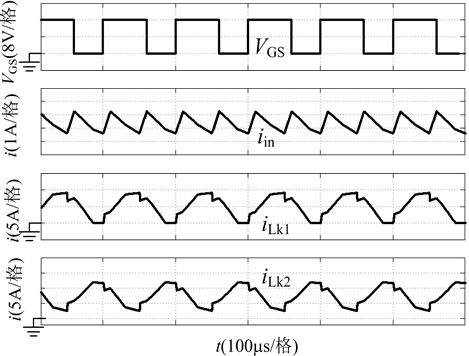 (a) 总输入电流波形及电感l1、l2的电流波形
(a) 总输入电流波形及电感l1、l2的电流波形  (b) 开关管q的驱动波形及其对应的电压仿真波形
(b) 开关管q的驱动波形及其对应的电压仿真波形  (c) 二极管d1、d2、d3、do的电压仿真波形
(c) 二极管d1、d2、d3、do的电压仿真波形 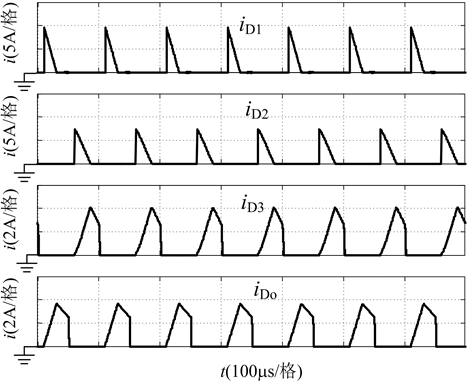 (d) 二极管d1、d2、d3、do的电流仿真波形
(d) 二极管d1、d2、d3、do的电流仿真波形
. simulation waveforms
图8. 仿真波形
2/5,二极管do上的电压应力近似等于输出电压vo的3/5;图8(d)中分别为二极管d1、d2、d3、do的电流仿真波形,可以看出二极管d1、d2实现零电流关断。仿真结果与上述理论分析一致,验证了该拓扑结构的正确性和有效性。
由理论分析和仿真结果表明,本文所提出的变换器既实现了较高的电压增益,有效降低了功率器件的电压应力,同时又继承了传统交错并联dc/dc变换器输入电流纹波小的优点,因此在低压、大电流输入,高电压输出的应用场合是一个可取的选择。
5. 结论
本文提出了一种基于三态开关的高增益dc/dc变换器拓扑,首先采用双耦合电感的一次绕组分别替代传统交错并联dc/dc变换器的两个分立电感,同时引入由耦合电感二次绕组串联后与开关电容一起构成的电压倍增单元,再与二极管–电容技术相结合,进一步提高了变换器电压增益。其次,输入端采用交错并联结构,减小了开关器件的电压应力,实现了电流扩容和纹波抑制。输出端采用一个二极管整流结构。从理论分析以及仿真结果,可以看到该变换器具有输出电压增益高、功率器件电压应力低、输入电流纹波低等优点,因此适合用在低压、大电流输入、高电压输出的应用场合。
基金项目
河海大学文天学院科学研究项目(wt15005zd)。