1. 引言
光子灯笼是一种全光纤结构的线性光学器件,由多根单模光纤经拉锥而成 [1] [2] ,光子灯笼最早应用在天文学光谱滤波和空分复用(sdm)领域。目前人们将光子灯笼应用于光纤横模(模式)的自适应空间控制中 [3] ,并表现出了其独特优势。基于光子灯笼模式自适应控制,实现了对高功率光纤激光的模式不稳定(tmi)的控制,实验结果显示光子灯笼模式自适应控制可以大大提高tmi的阈值 [4] 。模式的自适应控制,在激光应用具有重要应用,比如:激光切割技术中有时需要环形光束进行钻孔 [5] ;基于空分复用的光通信系统需要利用高阶模式以提高通信容量 [6] ;对于高功率激光器,希望得到接近衍射极限的基模光束 [7] 等。
用于模式控制的光子灯笼,与最早用于天文光谱测量中的光子灯笼在结构上不同,如图1所示。用于模式控制的光子灯笼其形状与合束器类似,但光子灯笼的拉制要求更高,除了满足绝热近似要求外,还对输出模式与合束输入端单模光纤数以及排布有严格要求 [6] 。光子灯笼的输入端单模光纤的输入光初始相位、振幅等参量,对光束在光子灯笼中的演化和输出模式产生严重影响。为了分析光子灯笼中输入各通道的功率占比(振幅)、相位和偏振,对输出的耦合效率和光束质量的影响,本文中第二节将介绍光子灯笼中的结构与模式关系、模式相干叠加的一般理论、光束质量m2的理论计算方法。第三节主要通过数值计算,分析输出光斑形态、耦合效率和光束质量随模式间相位差、功率占比以及偏振的变化规律,并分析输入端振幅、相位和偏振对光子灯笼模式控制的影响。
2. 基本原理
2.1. 光子灯笼结构与模式
为了使光子灯笼能对输出模式进行控制,光子灯笼的拉制在满足绝热条件的同时,其输入端单模光纤数与输出端结构的等效v数有一定的要求,这是由于多模光纤中v数与光纤中可以存在的模式数有一定的对应关系。因此光子灯笼中输出端由等效v数所确定的可以存在的模式数与输入端单模光纤数必须相等 [1] [7] [8] ,图2从物理图像上表示了这种关联,例如当等效v数大于3.83而小于5.13时(图中第三行),对应输出端可以存在的6个模式(图中第二行),则输入端单模光纤数应为6路,且其排布也有要求,以降低损耗 [6] ,如图中第一行所示。因此,光子灯笼在制作过程中,输入端的单模光纤数、以及几何排布必须满足一定规则,如图2所示。
2.2. 模式相干叠加的一般理论
由于光子灯笼中存在的
模具有正交性、叠加性,当相干光注入系统时,在光纤不太长或经过光
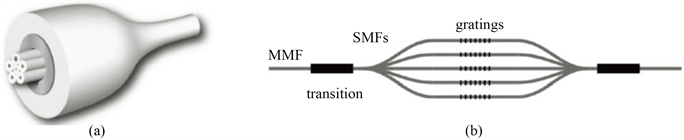
. (a) photonic lanterns in mode controlling system. (b) photonic lanterns in astronomical measuring system
图1. (a) 光纤模式控制中的光子灯笼,(b) 天文测量中光学滤波光子灯笼。

. (a) coupled waveguide arrays. (b) 15 lowest order step index fiber spatial modes. (c) normalized frequency v
图2. (a) 耦合波导阵列。(b) 阶跃光纤前十五个空间模式。(c) 归一化频率v
程补偿的条件下,这些
模式是相干的,此时输出光场可写为 [9] :
(1)
其中
是在相干叠加过程中
模式的功率占比,在实际系统中,受到环境的影响,输入振幅会发生随机变化,进而引起
的变化,当然,也可以通过外加的控制对各通道输入的振幅进行调节。
是
模式的相位,由三部分构成,即
,
为
模式在传输过程中产生的相位,可由
计算得来(其中
为
模式的传播常数,l为
模式的传播距离);
为
模式的随机相位变化;
为控制系统外加的相位。另外,考虑到一些
模式存在两个偏振态,故偏振也可能是影响叠加光场的因素之一。
在光子灯笼各通道进行耦合时,振幅和相位对耦合效率的影响如下 [3] :
(2)
其中,
是光子灯笼第m通道的功率,在小振幅误差条件下,耦合损耗
与
成正比,其中p为每个通道的标称功率,
为输入通道功率的标准差;相似地,随机相位变化(
)对耦合损耗的影响也满足
。
2.3. 光束质量m2的理论计算方法
m2因子是一种应用广泛且被大家所接受的光束质量评判参数 [9] ,能够反映光束在传输过程中的质量特性 [10] 。20世纪90年代初,a.e.siegman引入空间频率和强度矩的概念,总结出基于二阶强度矩的m2因子计算方法。以
方向为例,设一光束的光场用
表示,则其对应的空间频谱为
,则该光束的m2因子可表示为:
(3)
其中二阶强度矩σx和σs分别为:
(4)
而
和
分别为空间和频域的重心:
(5)
根据式(3)可以数值计算输出光束的
和
,实现对光束质量的评价,并为后续控制算法的评价函数提供依据。
3. 仿真结果及分析
3.1. 耦合结果随影响因素的变化规律
从两个
模式的相干叠加数值计算入手,得到输出光斑形态、耦合效率和光束质量随模式间相位差、功率占比以及偏振的变化规律。
以
模式和
模式的相干叠加为例,根据式(1)可知,
模式和
模式(暂不考虑偏振)相干叠加的光场表达式为:
(6)
3.1.1. 模式间相位差对耦合结果的影响
假设两模式耦合时,
模式和
模式的功率占比和偏振状态固定,而两模式间的相位差
从小到大变化(这里只考虑确定的相位差,而不考虑随机抖动的相位变化)。例如:当
模式和
模式的功率占比为4:1保持不变,且
模式只考虑一个偏振态时,可以得到叠加结果随
的变化,如图3所示。
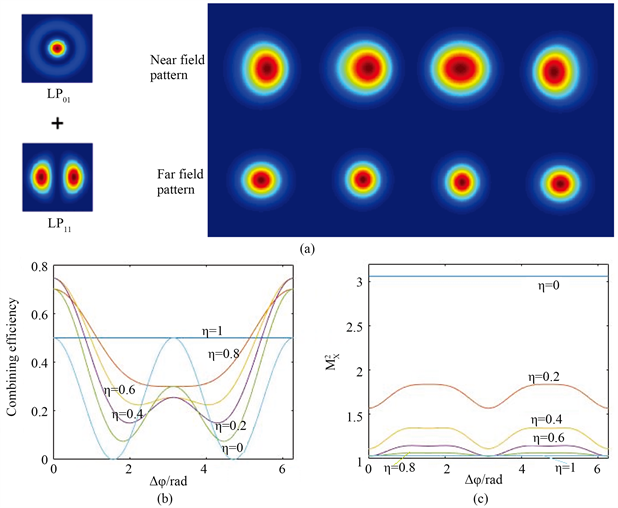
. (a) near- or far-field pattern, (b) δφ-combining efficiency diagram, (c)
diagram, with the increasing of
when
and
coherent
图3.
模式和
模式相干叠加时,随着
的增加:(a) 近场和远场的光斑图像,(b)
-耦合效率曲线图,(c)
曲线图
可见,耦合效率和m2因子随相位差
的变化是周期性的,且周期为π。特别地,当高阶模成分比较低时,可以通过控制
,很好的的提高光束质量。
3.1.2. 模式功率占比对耦合结果的影响
考虑功率占比h对叠加结果的影响:假设两模式耦合时,
模式和
模式的相位差和偏振固定,而两模式的功率占比变化。比如:当
模式和
模式的相位差为0,
模式只考虑一个偏振态时,可以得到叠加结果随h的变化(如图4所示)。
可以看到,
且
时,耦合效率随
的增加而降低。同时, 也随
的增加而降低,且类似抛物线型,说明随着高阶模成分的增加,光束质量越差。
也随
的增加而降低,且类似抛物线型,说明随着高阶模成分的增加,光束质量越差。
3.1.3. 偏振对叠加结果的影响
将上述参与耦合的单偏振的
模式更替为两个偏振态
模式的组合,通过数值计算发现:
模式和
模式的占比不同时,得到的光斑形态不同,但与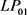 模式耦合后的效率以及m2因子的数值并没有改变。
模式耦合后的效率以及m2因子的数值并没有改变。
综上,在两个
模式相干叠加时:相位差对耦合效率和m2因子的影响是周期性的;高阶模功率占比提升会使光束质量迅速下降;偏振会改变相干叠加的光斑形态而不影响光束质量;m2因子相同的输出可能对应着不同相位和功率占比的组合。
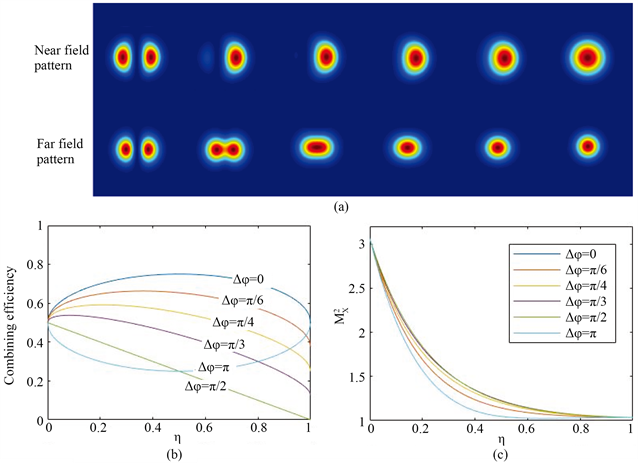
. (a) near- or far-field pattern, (b) h-combining efficiency diagram, (c)
diagram, with the increasing of h when
and
coherent
图4.
模式和
模式相干叠加时,随着h的增加:(a) 近场和远场的光斑图像,(b) h-耦合效率曲线图,(c)
曲线图
3.2. 三通道光子灯笼中的模式控制
上一节展示了振幅、相位、偏振对叠加结果不同程度的影响。结合2.1中的理论,以及三通道和六通道光子灯笼实际参数,进行仿真计算,得到光子灯笼单模输入端的振幅、相位和偏振对输出端模式控制的影响。
三通道光子灯笼是由三根单模光纤拉制而成,其输出模式为
、
和
三个模式,如图2所示。由于三根输入单模光纤间的相位、振幅等因素的影响,其光子灯笼的输出呈现出不稳定模式变化,其变化表现为
、
和
三个模式叠加行为 [3] 。我们对其变化规律进行了数值计算,图5(a)显示了三通道的光子灯笼中
模式、
模式和
模式叠加时,光束质量与各模式功率占比的关系,依然符合高阶模含量越高,光束质量越差的基本规律,通过提升耦合过程中基模的功率占比,可以使输出端的光束尽量靠近基模状态;图5(b)显示了
模式和
模式相对
模式间的相位差对光束质量产生的影响,此时m2因子随相位的变化仍是周期性的,且在
,k为整数时,取到极小值。结合图5(a)、图5(b)可知,欲使输出端的模式控制在基模状态(m2因子较小)上,至少要同时控制参与耦合模式的振幅和相位两个变量。
在三通道的光子灯笼中,假设输入段光场已按不同模式传播了距离l,则其耦合前已存在的
可以按照
的方式来计算。因此要控制各通道相位使得
(其中为整数),此时耦合效率和光束质量都能得到较好的值,光斑形态基本成基模样式。而对于功率占比的控制,应在保证基膜含量较高的前提下,把控制重点放在减小功率随机变化量上(即减小
),以提高整个器件的耦合效率。

. (a)
diagram, (b)
diagram, when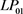 ,
and
coherent
,
and
coherent
图5.
模式、
模式和
模式相干叠加时,(a)
图h (b)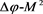 图
图
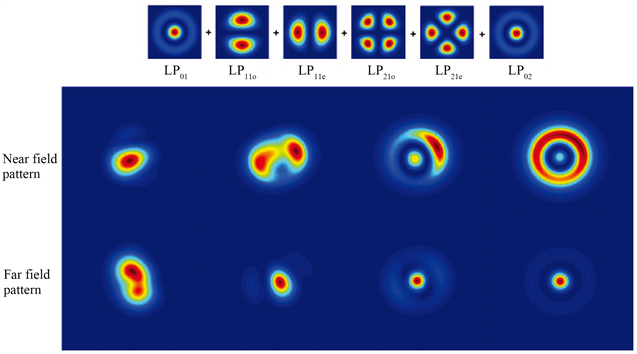
. different near- or far-field pattern when the modes coherent in the six-channel photonic lantern
图6. 六通道光子灯笼中存在的模式相干叠加时形成的不同光斑形态
当光子灯笼扩展到六通道时,不同叠加方式形成的光斑形态更为丰富,给模式控制得到的结果提供了更多可能。六通道光子灯笼是由六根单模光纤拉制而成,其输出应为六个模式如图2所示。在图6中第一行给出了六通道光子灯笼中可以输出的六个模式,第二行给出了六通道输入经演化耦合后,输出可能出现六个模式叠加的光斑形态。
依旧以控制输出到基模状态为例:当同时改变六个通道的相位和功率占比时,我们可以得到的最优的光束质量
在2.03附近,该值在
较高、
或p或2p时取到;而当
,
,
,
,
,
时,控制相位在0或p或2p附近的合适且相对稳定的值时,可以使
,此时对应的
,保证了可接受的耦合损耗,得到的光斑形态也与基模相一致。这说明光子灯笼能够通过控制输入端的振幅、相位等因素,实现输出端的模式控制。
4. 结论
本文主要讨论了光子灯笼中存在的模式在相干叠加的模型下,不同模式间的相位差、功率占比以及偏振对耦合效率h和光束质量m2因子的影响,分析了光子灯笼如何对输入端进行控制以实现输出端的模式控制。通过以上工作,我们得出:耦合效率h和光束质量m2因子的数值随基模功率占比
的增加而降低;而随着模式间相位差的改变,耦合效率h和光束质量m2因子呈周期性变化。将以上结果应用在光子灯笼的模式控制中,需要同时控制光子灯笼输入端的功率占比和相位两个变量,且在得到较为理想的输出(比如m2因子较低的基模)后,要尽量减小这两个变量的标准差(
,
),以提升耦合效率。若要利用光子灯笼实现特殊光斑的输出,则需同时控制振幅、相位以及偏振三个因素,并在控制系统中对评价函数进行特殊地设定。