摘要:
运用多项有序逻辑回归分析的方法,建立模型,通过平时学习情况对大学生成绩等级进行分析预测,结果表明,有考研计划、听课认真情况以及高考数学成绩会对大学生数学成绩趋于优秀有较大的影响,自觉做作业和整理笔记对大学生期末数学成绩没有较大的促进作用,课前适当程度的预习对大学生数学成绩有一定的帮助,同时模型预测准确度达51.69%。
abstract:
by using the method of multiple ordered logistic regression analysis for modeling, through the usual learning situation, college students’ performance rating has been predicted and analyzed. the results show that plan for postgraduate entrance examination, careful listening in class and mathematics result of college entrance examination will have a greater impact on college students’ math scores tending to be excellent. consciously doing homework and taking notes have no significant effect on the final math scores of college students, while properly previewing before class helps in the scores. at the same time, the model prediction accuracy can reach 51.69%.
1. 引言
肖婕 [1] 等应用方差法分析了生源地、任课教师等因素对大学数学、英语成绩的影响,宁静 [4] 等应用聚类法分析了高考总分对大学数学、英语成绩的影响,王亮红、彭慧芹 [2] 应用聚类分析法探讨了聚类分析技术在教学管理中的应用,白春玲 [3] 等应用广义线性回归模型研究了学生学年间成绩的相关性。本文研究大学生数学成绩与高考成绩、考研意向、课堂表现等诸多影响因素之间的相关性,与以往研究相比,范围较为集中,主要考虑学业方面的因素,以山东理工大学财管、市销和金融三个专业的学生为调查对象,设计调查问卷,回收有效问卷239份。
2. 逻辑回归分析的假设检验
使用有序logistic进行回归分析时,需考虑四个假设:1) 因变量唯一,且为有序多分类变量;2) 存在一个或多个自变量,可为连续、有序多分类或无序分类变量;3) 自变量之间无多重共线性;4) 模型满足“比例优势”假设。
直接将分类变量纳入logistic回归方程,则软件会将分类变量按连续变量处理。例如,按“文科”——1,“理科”——2进行编码,纳入方程,方程会认为“理科”是“文科”的两倍,所以,为了解决这个问题,在对假设进行验证之前,需要用一系列的二分类变量“是”或“否”来表示原始的分类变量,这些新的二分类变量称为“哑变量”。下面我们对假设进行判断,此处重点分析假设3~4。
见表1,容忍度均远大于0.1,方差膨胀因子均小于10,所以不存在多重共线性。
a. 因变量:等级。
见表2,平行线检验中卡方 = 46.678,p = 1,大于0.05,说明平行性假设成立,即各回归方程相互平行,可以使用有序logistic过程进行分析。
. test of parallel lines
表2. 平行线检验c
零假设规定位置参数(斜率系数)在各响应类别中都是相同的。
a. 在达到最大步骤对分次数后,无法进一步增加对数似然值。
b. 卡方统计量的计算基于广义模型最后一次迭代得到的对数似然值。检验的有效性是不确定的。
c. 联接函数:logit。
3. 多项有序逻辑回归分析
对模型中所有自变量的偏回归系数是否全为0进行似然比检验,判断模型拟合程度。
原假设为所有纳入自变量的系数为0,我们所得出的模型拟合信息表(表3)中显著性小于0.05,说明至少有一个变量系数不为0,且具有统计学显著性即模型整体有意义。换言之,拟合自变量的模型拟合优度好于仅包含常数项的模型。
. model fitting information
表3. 模型拟合信息
联接函数:logit。
根据spss使用的模型以及参数估计值表格,可以列出方程:
上述三个方程参数只在阈值上有差别。在控制了高考成绩的条件下计算出
。可以由此得出取得优秀、良好、及格、不及格的可能性,从而我们可以对大学生的等级数学成绩进行预测。例如,由第一位学生各项数据我们计算出
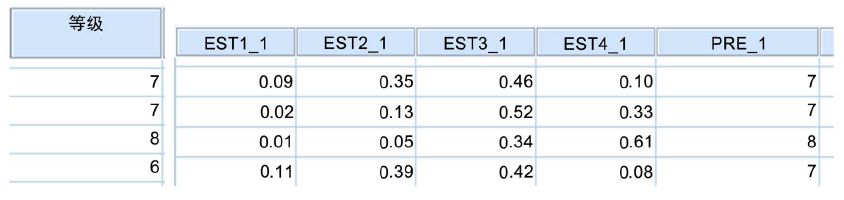
,可见,该学生数学成绩等级为5 (不及格)的可能性为9%,数学成绩等级为6 (及格)的可能性为35%,数学成绩等级为7 (良好)的可能性为46%,数学成绩等级为8 (优秀)的可能性为10%,综合分析,该生的成绩等级预测结果为7 (良好)。利用该逻辑回归模型对大学生数学成绩等级进行预测,图1为对大学生数学成绩等级的预测结果部分图。
. partial diagram of the prediction results of college students’ mathematics grades
图1. 大学生数学成绩等级的预测结果部分图
est1_1、est2_1、est3_1、est4_1代表四个成绩等级的预测概率。其中第一行中est3_1概率最大,为0.46,对应的pre_1为7 (良好),因变量成绩等级的观察值也为7 (良好),此时模型准确地预测了因变量。而第四行中est3_1最大,预测的pre_1为7 (良好),而因变量的实际的观察值为6 (及格),此时模型没有准确地预测因变量。
为明确该模型的预测效果,建立等级*预测响应类别交叉制表。表4显示,成绩等级为5 (不及格)时,
. rank*pre_1 predicted response category cross tabulation
表4. 等级*预测响应类别交叉制表
模型预测正确的有1人(16.7%),同理,成绩等级为6 (及格)、7 (良好)、8 (优秀)时,模型预测正确的分别有3人(13.6%)、34人(66.7%)、23人(59%)。根据预测响应类别交叉制表可计算出模型预测的总准确度为(1 3 34 23) ÷ 118 = 51.69%。
4. 结论
综上所述,是否有考研计划、听课认真情况及高考数学成绩对大学生数学成绩是否趋于优秀有较大的影响,自觉做作业和整理笔记对大学生期末数学成绩没有较大的促进作用,课前适当程度的预习对大学生数学成绩有一定的帮助,且适当程度的预习比极为细致的预习有更好的效果,预习过于细致可能会在课堂上稍加松懈,对老师课堂上的传授不会过多在意,该行为会导致学习效果不佳。
参考文献
notes
*通讯作者。