1. 引言
我国作为制造业大国,拥有众多劳动密集型的制造行业,员工是生产链中必不可少的一环,企业能否高效完成生产活动来应对产品的巨大需求很大程度上取决于制造企业员工的生产和交付绩效,及时有效地对员工生产效率进行分析和预测可以帮助企业管理者更好地做出决策,进而制定更加合理、先进的管理和生产模式 [1] 。
关于员工生产效率的研究,可大致分为理论探讨和实例研究两方面。理论探讨方面,jose l. zofio和angel m. prieto (2007)通过数据包络分析(dea)评估投入产出框架中的生产效率 [2] 。尚倩(2013)进行了基于心理负荷的生产效率研究,深度挖掘了情绪和心态疲劳等心理负担对员工生产效率的影响 [1] 。novotná m.和volek t. (2015)分析了生产要素效率与农业企业财务绩效之间的相关性 [3] 。张晓洁(2019)阐述了员工在企业中扮演的角色及其特点,提出可以从物质、精神、反向激励和定期沟通等方面来提高员工的积极性及其生产效率 [4] 。实例研究方面,徐晓波(2016)以k公司生产线员工的工作绩效为研究对象,分析其影响因素并给出了提升方案 [5] 。牛金凤(2021)探究了内蒙古光伏企业的生产效率及其影响因素,从提高企业能力与改善外部环境两方面提供了生产效率优化建议 [6] 。纵观国内外学者对于员工生产效率的研究,大多是从理论层面来进行定性分析,少有针对具体案例的量化研究。因此,本文选择针对实例进行量化分析,研究内容一定程度上可以丰富该领域的现有成果。
服装业是现代化工业的典例之一,也是我国重要的高度劳动密集型产业,手工流程多,因此将服装产业的员工生产效率作为研究对象具有很强的代表性。本文根据uci数据库中的productivity prediction of garment employees data set,挖掘影响服装厂员工生产效率的各类因素,并使用机器学习进行生产效率分类预测,进而为企业优化生产效率提供指导。
2. 理论基础
2.1. 支持向量机
支持向量机(svm)是一种广义线性分类器,其主要工作是寻找在特征空间上的最大间隔超平面,对于线性不可分的样本可通过核技巧转化为线性可分问题。如图1所示,
即为分隔超平面,这样的分隔超平面有多个,但几何间隔最大的超平面只有一个。
假设给定一个特征空间上的训练样本集
,其中
,
为第i个特征向量,
为标签, 1和‒1对应正例和负例的取值。在线性可分的情况下,对于s和超平面
,定义超平面的间隔为

. schematic diagram of svm
图1. 支持向量机原理图
(1)
超平面关于s中所有样本点的最小几何间隔为
(2)
求得最大分隔超平面的问题转化为以下约束最优化问题 [7] :
(3)
(4)
2.2. 核密度朴素贝叶斯
朴素贝叶斯分类是一种基于概率论的分类算法,在实际情况中,特征变量之间可能存在相关关系,并且当不同特征变量的分布呈现非离散和多态时,朴素贝叶斯分类算法往往会出现问题。因此,基于核密度估计的朴素贝叶斯算法被提出。
核密度估计是一种非参数概率估计方法,其表达式为 [8]
(6)
其中,
是随机变量x的p个样本,h为平滑参数,
为核函数。本文中使用的核函数为box核函数,其表达式如下
(7)
2.3. 随机森林
随机森林作为bagging算法的代表具有较强的泛化能力,适合处理大规模数据,还可以衡量各个特征的重要性。随机森林是由多棵子决策树组成的集成分类器,在特征变量和样本的选择上具有随机性,其最终输出的类别是子决策树输出类别的众数。随机森林的参数设置会极大影响其性能,决策树的数目是模型最重要的参数之一。树的数量过少,模型的学习效果欠佳,容易陷入欠拟合。树的数量增加到一定程度后,模型的表现不会有显著的提升,运行负担加重,甚至存在过拟合风险。
3. 服装厂员工生产效率预测建模
3.1. 数据来源及变量介绍
本文的数据来自uci数据库中的productivity prediction of garment employees data set (服装厂员工生产效率预测数据集),原始数据提供了某服装厂2015年1月到2015年3月的1197条日度数据,共有15个变量。本文从中筛选出1160个有效样本,将工人的实际生产效率actual_productivity作为待预测的目标变量。考虑到员工的工作状态主要由外部环境与内在精神两方面决定,本文从物质激励、工作负荷、生产事故、目标促动这四个反映外部生产环境、影响员工内在情绪的维度筛选出7个特征变量构造初始指标体系来对目标变量实际生产效率进行预测,如表1所示。物质激励有利于调动员工生产积极性,使员工心情愉悦,工作热情高涨从而提高实际生产效率。工作负荷方面,服装样式更改意味着计划外的生产工作,任务所需时间和加班时间过长会增加劳动强度,这都有可能引起员工的不满情绪,导致实际生产效率降低。生产事故的发生会打乱原有生产节奏,对实际生产效率带来负面影响。目标生产效率对实际生产效果具有导向作用,员工会根据每日给定的目标来调整工作强度,适宜的目标能够给员工一定的压力从而减少其怠慢工作的可能性。
. initial indicator system
表1. 初始指标体系
3.2. 建模流程
服装厂员工生产效率预测建模流程如图2所示。本文首先从物质激励、工作负荷、生产事故、目标促动四个维度选择出7个初始特征变量和1个目标变量,构造了多维指标体系来对目标变量实际生产效率进行预测。其次对样本进行缺失值和离群值处理,应用斯皮尔曼相关系数法进行特征筛选,得到最终样本和最终特征变量。最后利用机器学习模型进行预测。
3.3. 数据预处理
3.3.1. 缺失值、离群值处理
首先利用spss对样本数据进行缺失值检测,无缺失值。其次使用spss和matlab对样本数据进行离群值检测和描述统计分析,统计分析表和箱线图如表2、图3所示。
由表2和图3可以看出,变量targeted_productivity、over_time、incentive、idle_time、idle_men、no_of_style_change和actual_productivity这7个变量存在离群值。

. modeling process
图2. 建模流程图

. boxplots
图3. 箱线图
. statistical analysis table
表2. 统计分析表
对于over_time变量,离群点只有一个,值为25,920,这与其它值相差过大,所以应当剔除;对于incentive变量,物质激励不会每日发放,离群点共有10个,但物质激励金额高于一般取值的原因很可能与领导者的决策有关,例如发放福利来调动员工积极性,因此incentive变量的离群点予以保留。对于idle_time变量,离群点共有18个,工厂绝大部分时候都处于正常运转常态,出现事故的次数很少,因此idle_time的取值大都为0,而一旦出现事故,其造成的停工时长难以确定,实际生产中必须考虑意外的发生,因此idle_time的离群点属于自然离群点,予以保留;对于idle_men变量,离群点共有18个,其与idle_time离群点出现的日期完全一致,当生产正常进行时,所有工人都会有分配的任务需要完成,因此idle_men取值也大都为零,而当意外发生时,部分工人的工作无法进行而处于闲置状态,闲置工人的数量也与事故的严重程度密切相关,数量难以确定,因此idle_men的离群点属于自然离群点,予以保留。对于no_of_style_change变量,离群点共有147个,统计可得该变量的取值只有0、1和2三个,且绝大多数工作日的取值都为0。工厂的运作按照生产计划执行,服装样式都已事先规定,当客户需求突变或者原材料供应出现问题时,工厂才会被迫更改既有服装样式,并且样式更改次数一日内不会过多,因此no_of_style_change离群点属于自然离群点,予以保留。对于actual_productivity变量,离群点共有62个,最小值为0.233705476,造成实际生产率低下的原因有多种,这也是本文需要重点关注的部分,因此actual_productivity的离群点予以保留。最后,对于targeted_productivity变量,离群点共有79个,下邻为0.6,最小值为0.07。目标生产效率为0.07显然不符合实际,另外根据马斯洛需求理论和员工激励理论,员工在工作中还有自我实现和自我超越的需求,过低的目标不利于调动员工的生产积极性,反而会削弱员工的生产力。由表2可得,actual_productivity的均值为0.726,在工厂实际生产率普遍不低的情况下,管理者制定过低的目标生产效率的做法并不可取,在实际情况中应当避免,因此targeted_productivity的离群点予以剔除。
经过缺失值和离群值处理,共剔除79个样本,最终得到1081个样本。
3.3.2. 特征筛选
本文选择斯皮尔曼相关系数法来进行特征筛选,目标变量与各个特征变量的相关系数值和显著性如表3所示。由表3可得targeted_productivity、incentive与actual_productivity呈显著正相关,smv、over_time、idle_men、idle_time、no_of_style_change与actual_productivity呈负相关,这与实际情况相符。
. spearman correlation coefficient
表3. 斯皮尔曼相关系数
本文通过p值显著性来筛选出与目标变量相关关系显著的特征变量,over_time的p值为0.197,与目标变量的相关关系不显著,因此予以剔除。最终指标体系如表4所示。
. final indicator system
表4. 最终指标体系
3.3.3. 数据归一化
为了消除量纲的影响,需要进行归一化处理,本文采取min-max标准化,将特征变量的值映射到[0, 1]区间内,变换函数如下
(8)
其中, 为某一特征变量的取值, 为该特征变量的最大值, 为该特征变量的最小值。
3.4. 类别划分及模型评估指标
为了便于后续机器学习的分类预测,本文将目标变量actual_productivity按照范围分成高效和非高效两类,由于targeted_productivity的中位数为0.75,因此将actual_productivity取值不超过0.75的归为非高效,记为类别1,将取值大于0.75的归为高效,记为类别2。
为了衡量模型的泛化能力,本文将模型在测试集上的分类正确率作为衡量模型性能的指标。
(9)
为分类正确率,
为实际类别为i,预测类别为
的样本个数,测试集分类正确率越高,表明模型的泛化能力越强。
4. 实验结果与分析
本文将1081个样本随机打乱,按照7比3的比例划分训练集和测试集,将前756个样本作为训练集,后325个样本作为测试集。
4.1. 各模型的参数设置与实验结果
4.1.1. 各模型的参数设置
本文利用matlab 2022a和libsvm来进行实验,对于支持向量机模型,核函数的选取对模型有较大的影响,因此本文分别建立了linear-svm、poly-svm、rbf-svm和sigmoid-svm模型,其参数设置如表5所示。对于核密度朴素贝叶斯模型,kernel选择box,其余参数选择默认。对于随机森林模型,其参数设置如表6所示。
. parameters of svm
表5. 支持向量机参数设置
. parameters of random forest
表6. 随机森林参数设置
4.1.2. 各模型的实验结果
为了降低偶然性,将程序运行10次,取10次分类正确率的平均值作为模型的最终分类正确率,各模型的结果如表7所示。可以看出随机森林的表现最好,分类正确率达到了83.2000%,其次是linear-svm、rbf-svm、sigmoid-svm,分类正确率分别为75.6308%、75.3846%和75.4872%,核密度朴素贝叶斯模型和poly-svm表现最差,分类正确率只有62.6462%和61.9081%。通过比较各模型的分类正确率可以看出,采用集成算法的随机森林模型的表现明显优于支持向量机、核密度朴素贝叶斯两个单一分类模型,体现了集成算法的优越性。
. result of each model
表7. 各模型实验结果
4.2. 随机森林参数优化
树的数目是随机森林最重要的参数之一,树的数量过多容易陷入过拟合且对模型效能的提升作用不大。但是,树的数量过少则会导致欠拟合,模型的学习力度不够。因此本文在保证泛化能力的前提下尽量减少树的数目来实现模型的优化。
随机森林的袋外误差ooberror是对泛化误差的无偏估计,因此本文根据ooberror的变化情况选择合适的树的数目,图4为随机森林的ooberror变化情况,可以看出,当树的个数增加到100以后,ooberror的值基本处于稳定,因此本文在随机森林初始模型的基础上将树的数目从500改为100,得到参数优化后的最终模型。

. change of ooberror
图4. ooberror变化
将随机森林的优化模型运行10次,得到的测试集平均分类正确率达到了83.8461%。与初始模型相比,优化模型的分类正确率略有提升,证明参数优化是有效的。
4.3. 随机森林特征重要性分析
为了进一步挖掘影响实际生产效率的因素,本文通过参数优化后的随机森林模型的特征重要性来进行更深入的分析。参数优化后的随机森林模型得出的6个最终特征变量重要性如图5所示,根据特征贡献度,重要性排名前三的特征变量依次为targeted_productivity,incentive和smv。而no_of_style_change、idle_men和idle_time属于发生概率较小的意外事件,对日常实际生产效率的影响总体不大。因此在实际生产过程中,工厂管理者应当注重制定合理的目标和生产计划,并关注员工的心理状态,可适当采取物质激励和精神激励相结合的方式来提高员工的工作积极性。
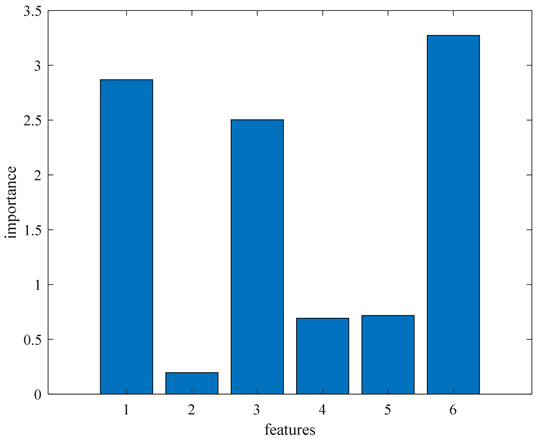
. feature importance
图5. 特征重要性
5. 结语
本文对uci数据库中的服装厂员工生产效率数据进行了研究,建立了多种机器模型来对实际生产效率进行预测。其中随机森林测试集分类正确率最高,为83.2000%。为了降低过拟合风险和减轻运行负担,本文对初始随机森林模型的树的个数进行了优化,优化后的随机森林测试集分类正确率达到了83.8461%,模型的泛化能力有所提升。
最后,本文根据随机森林模型的特征重要性分析得出影响实际生产效率的最重要的三个因素依次为目标生产效率、物质激励和分配的任务时间。这对同服装厂类似的劳动密集型企业具有一定借鉴意义。