非线性薛定谔方程解的同伦分析-凯发娱乐官网

期刊菜单

非线性薛定谔方程解的同伦分析
solutions of the non-linear schr?dinger equation based on the homotopy analysis method

doi: , , html, , 国家自然科学基金支持
作者: 徐扬, 单可, 梁雨珂, 吴颉尔, 周昱^*：江苏科技大学理学院，江苏镇江；罗文琛：中南大学物理学院，湖南长沙
关键词: 非线性薛定谔方程；；周期解；同伦分析法；； soliton； periodic solution； homotopy analysis method

摘要: 同伦分析法是一种求解非线性演化方程的有效方法，本文研究了非线性薛定谔方程的同伦分析解。通过将方程化为耦合的方程组，给出了具有高次非线性和高阶色散的非线性薛定谔方程的孤子解和周期解，研究可给类似问题的求解提供有益思路。

abstract: homotopy analysis method is an effective method for solving nonlinear evolution equations. this paper studies the homotopy analysis solutions of nonlinear schrödinger equations. by converting the equations into coupled equation groups, it gives soliton solution and periodic solution for the nonlinear schrödinger equations with high-order nonlinearity and dispersion. the research may provide useful insights for solving similar equations.

文章引用：徐扬, 单可, 梁雨珂, 吴颉尔, 周昱, 罗文琛. 非线性薛定谔方程解的同伦分析[j]. 理论数学, 2024, 14(2): 527-538.

1. 引言

自然现象大多具有非线性，线性模型在描述客观实在时通常无法充分体现其遵循的变化规律，因此在数学上通过对非线性模型的研究来探索自然规律是重要且必要的。当方程的自变量与因变量之间的关系不满足线性关系时，方程称为非线性方程，通常包括非线性代数方程、微分方程、积分方程等，在科学研究和工程实际上具有非常广泛的应用。以非线性微分方程为例，不仅在基础数学领域具有重要意义，在应用领域还广泛存在于对航空航天、信息传递、生物现象、化学反应等许多复杂现象的研究中 [1] 。

非线性演化方程是描述系统随时间空间演化行为的一类非线性偏微分方程，通常可具有孤子解和周期解。在自然科学领域，孤波揭示了非线性作用引起的惊人有序性，两个孤波经过相互作用不改变形状、大小、速度和方向，但允许相位有变化，具有粒子性，所以也被称为孤子。近年来人们已建立了多种直接而有效的方法求解非线性演化方程，如hirota双线性导数法 [2] ，bäcklund变换 [3] ，adomian分解法 [4] ，ck直接法 [5] [6] ，darboux变换法 [7] ，wronskian技巧 [8] [9] ，(g’/g)-展开法 [10] [11] ，幂级数法 [11] [12] ，lie对称法 [13] ，反散射法 [14] ，齐次平衡法 [15] 等等。近年来，作为一种有效求解微分方程的方法，同伦分析法(homotopy analysis method，即ham)的提出在一些领域得到了广泛应用 [16] [17] [18] 。因为同伦分析法不依赖于特定的小参数，故而提供了自由选择参数的自由且提供了一个简单方法控制级数解的收敛性，显示出求解弱或强非线性方程的有效性 [19] [20] [21] [22] 。

非线性薛定谔方程(non-linear schrödinger equation，即nlse)是非线性演化方程中的一个重要模型，是量子力学中薛定谔方程的非线性拓展，展示如何在不满足线性叠加原理的情况下处理波动现象。这个方程在数学上对非线性动力系统、偏微分方程理论、复杂系统的数学建模等方面的研究具有重要意义，同时它又与非线性光学、冷原子物理、水动力学等许多实际问题密切相关，例如可以描述光纤中的光孤子、单色波的一维自调适、非线性光学的自陷、固体中的热传播、等离子体中朗缪尔波、超导电子在电磁场中运动、量子隧穿等，因此对该方程的研究不仅在理论上，而且在实际应用上都具有重要性。已有一些关于nlse的研究成果，包括利用ham求解的初步工作，但类似工作没有给出周期解 [23] 。

本文基于同伦分析法对非线性薛定谔方程的求解进行研究，第2节在简单介绍同伦分析的基本方法后，利用其求解标准的非线性薛定谔方程；第3节利用同伦分析给出对含有高次非线性和高阶色散的非线性薛定谔方程求解的基本步骤，然后在第4和5节分别针对孤子解和周期解进行研究；最后第6节给出文章的分析和总结。

2. 应用同伦分析法求解非线性薛定谔方程

2.1. 同伦分析法简介

考虑一般形式表示的非线性方程

$n [u (r, t)] = 0$ (2.1)

其中 $n$ 为非线性算子， $u (r, t)$ 为待求函数，r和t分别代表空间和时间变量。此时，将 $u_{0} (r, t)$ 假设为非线性方程的初始猜测解，这里的初始猜测解一方面要满足原非线性方程的边界条件，同时也要与所求的解形式相仿，这样才能得到更加精确的近似解。同理，我们可设一个辅助参数 $h \neq 0$ 以及一个辅助函数 $h (r, t) \neq 0$ ，定义辅助线性算子 $l$ 满足若 $f (r, t) = 0$ 则 $l (f (r, t)) = 0$ ，此时，把 $q \in [0, 1]$ 作为一个嵌入变量，可构造一个同伦

$\begin{array}{l} h [ϕ (r, t; q), u_{0} (r, t), h (r, t), h, q] \\ = (1 - q) {l [ϕ (r, t; q) - u_{0} (r, t)]} - q h h (r, t) n [ϕ (r, t; q)] \end{array}$ (2.2)

需要注意的是，如何选取适当的辅助参数h和辅助函数 $h (r, t)$ 对于同伦分析法起着至关重要的作用，直接决定了解的收敛性和有效性。正是由于辅助参数h和辅助函数 $h (r, t)$ 的引入，使得在选取初始猜测解 $u_{0} (r, t)$ 和辅助线性算子 $l$ 时我们可以有很大的选择空间。

令同伦(2.2)等于零可得

$h [ϕ (r, t; q), u_{0} (r, t), h (r, t), h, q] = 0$ (2.3)

得到零阶形变方程形如

$(1 - q) {l [ϕ (r, t; q) - u_{0} (r, t)]} = q h h (r, t) n [ϕ (r, t; q)]$ (2.4)

其中 $ϕ (r, t; q)$ 是原非线性方程的解，这不单取决于初始猜测解 $u_{0} (r, t)$ 的设定，而是辅助线性算子 $l$ 、辅助参数h、辅助函数 $h (r, t)$ ，以及嵌入变量q都联合作用于解的确定。

当我们令 $q = 0$ 时，零阶形变方程(2.4)就变为 $l [ϕ (r, t; 0) - u_{0} (r, t)] = 0$ ，由线性算子性质(2.2)可知

$ϕ (r, t; 0) = u_{0} (r, t)$ (2.5)

当令 $q = 1$ 时，由于 $h \neq 0$ 以及 $h (r, t) \neq 0$ ，零阶形变方程就变成所求的非线性方程

$n [ϕ (r, t; 1)] = 0$ (2.6)

假定

$n [ϕ (r, t; 1)] = u (r, t)$ (2.7)

从式(2.5)~(2.7)可以看到，当嵌入变量q从0连续增加到1的时候， $ϕ (r, t; q)$ 从初始猜测解连续变化成了非线性方程的解 $u (r, t)$ ，同伦理论中这种连续变化的过程称为形变。

既然存在零阶形变方程，则存在高阶形变方程。可以将零阶形变方程对q求导m次，再除以 $m!$ 后令 $q = 0$ ，就能得到与零阶形变方程对应的高阶形变方程

$l [u_{m} (r, t) - x_{m} u_{m - 1} (r, t)] = h h (r, t) r_{m} [u_{m - 1} (r, t)]$ (2.8)

其中

$x_{m} = {\begin{array}{l} 0, & m = 1 \\ 1, & m = 2, 3, 4, \dots \end{array}$ (2.9)

同时(2.8)中的

$r_{m} (u_{m - 1}) = \frac{1}{(m - 1)!} {\frac{\partial^{m - 1} n [ϕ (r, t; q)]}{\partial q^{m - 1}} |}_{q = 0}$ (2.10)

需要注意的是无论m的取值是否影响高阶形变方程的线性算子 $l$ ，这里的 $r_{m} (u_{m - 1})$ 都以通过定义的非线性算子 $n$ 给出且高阶形变方程的右端只与 $u_{m - 1}$ 相关，通过对高阶形变方程的观察，当m的取值从1到n时，可依次迭代出 $u_{1} (r, t), u_{2} (r, t), \dots$ 。在迭代n次之后可得 $u (r, t)$ 的n阶近似解

$u (r, t) \approx \sum_{k = 0}^{m} u_{k} (r, t)$ (2.11)

显然，高阶形变方程的左边只于线性算子有关，所以不难得到

$u_{m} (r, t) = x_{m} u_{m - 1} (r, t) \frac{h h (r, t) r_{m} [u_{m - 1} (r, t)]}{l}$ (2.12)

而由于线性算子 $l$ 具有的性质，故(2.12)式右端的 $l$ 只作用在 $r_{m} (u_{m - 1}, r, t)$ 的系数上，所以，确定了 $r_{m} (u_{m - 1}, r, t)$ 之后，就能通过(2.11)的累加，求出所需的n阶近似解。

以上介绍即为同伦分析法(homotopy analysis method，即ham)的概要。

2.2. 标准非线性薛定谔方程的求解

对于标准的(1 1)维非线性薛定谔方程，函数 $u (x, t)$ 满足如下形式

$i \frac{\partial u}{\partial t} α \frac{\partial^{2} u}{\partial x^{2}} β {| u |}^{2} u = 0$ (2.13)

式中 $α$ 代表群速度色散系数， $β$ 是非线性系数，令 $u (x, t) = v (x, t) i w (x, t)$ ， $v (x, t)$ 和 $w (x, t)$ 为实函数。代入上式得到

$\frac{\partial v}{\partial t} α \frac{\partial^{2} w}{\partial x^{2}} β (v^{2} w^{2}) w = 0$ (2.14)

(2.15)

初始条件下 $v (x, 0) = f_{1} (x)$ ， $w (x, 0) = f_{2} (x)$ ，进行行波变换，令 $ξ = x - c t$ ，

$v (x, t) = v (ξ), w (x, t) = w (ξ)$ (2.16)

选择初始孤子形式的猜测解为

$v_{0} (ξ) = 2 e^{- ξ} - e^{- 2 ξ}, w_{0} (ξ) = 2 e^{- ξ} - e^{- 2 ξ}$ (2.17)

得到

$\begin{array}{l} r_{m} (v_{m - 1}) = - \sum_{j = 0}^{i} c_{i - j} \frac{\partial v_{m - 1}}{\partial ξ} α \frac{\partial^{2} w_{m - 1}}{\partial ξ^{2}} β (\sum_{i = 0}^{m - 1} w_{m - 1 - i} \sum_{j = 0}^{i} v_{j} v_{i - j} \sum_{i = 0}^{m - 1} w_{m - 1 - i} \sum_{j = 0}^{i} w_{j} w_{i - j}) \\ r_{m} (w_{m - 1}) = - \sum_{j = 0}^{i} c_{i - j} \frac{\partial v_{m - 1}}{\partial ξ} α \frac{\partial^{2} v_{m - 1}}{\partial ξ^{2}} - β (\sum_{i = 0}^{m - 1} w_{m - 1 - i} \sum_{i = 0}^{i} v_{j} v_{i - j} \sum_{i = 0}^{m - 1} w_{m - 1 - i} \sum_{i = 0}^{i} w_{j} w_{i - j}) \end{array}$ (2.18)

随后解得

$\begin{array}{l} v_{1} (ξ) = - e^{- 2 ξ} 2 e^{- ξ} \frac{2}{35} e^{- 6 ξ} h - \frac{1}{2} e^{- 5 ξ} h \frac{8}{5} e^{- 4 ξ} h - 2 e^{- 3 ξ} h \frac{32}{35} e^{- 2 ξ} h - \frac{1}{14} e^{- ξ} h \\ v_{2} (ξ) = - e^{- 2 ξ} 2 e^{- ξ} \frac{4}{35} e^{- 6 ξ} h - e^{- 5 ξ} h \frac{16}{5} e^{- 4 ξ} h - 4 e^{- 3 ξ} h \frac{64}{35} e^{- 2 ξ} h - \frac{e^{- ξ} h}{7} \\ - \frac{4 e^{- 10 ξ} h^{2}}{3465} \frac{51 e^{- 9 ξ} h^{2}}{2800} - \frac{268 e^{- 8 ξ} h^{2}}{2205} \frac{13}{30} e^{- 7 ξ} h^{2} - \frac{35792 e^{- 6 ξ} h^{2}}{42875} \frac{521}{840} e^{- 5 ξ} h^{2} \\ \frac{564}{875} e^{- 4 ξ} h^{2} - \frac{103}{70} e^{- 3 ξ} h^{2} \frac{3470633 e^{- 2 ξ} h^{2}}{4244625} - \frac{7136879 e^{- ξ} h^{2}}{67914000} \\ v_{3} (ξ) = \dots \end{array}$ (2.19)

以及

$\begin{array}{l} w_{1} (ξ) = - e^{- 2 ξ} 2 e^{- ξ} - \frac{2}{35} e^{- 6 ξ} h \frac{1}{2} e^{- 5 ξ} h - \frac{8}{5} e^{- 4 ξ} h 2 e^{- 3 ξ} h - \frac{32}{35} e^{- 2 ξ} h \frac{e^{- ξ} h}{14} \\ w_{2} (ξ) = - e^{- 2 ξ} 2 e^{- ξ} - \frac{4}{35} e^{- 6 ξ} h e^{- 5 ξ} h - \frac{16}{5} e^{- 4 ξ} h 4 e^{- 3 ξ} h - \frac{64}{35} e^{- 2 ξ} h \frac{e^{- ξ} h}{7} - \frac{4 e^{- 10 ξ} h^{2}}{3465} \\ \frac{51 e^{- 9 ξ} h^{2}}{2800} - \frac{268 e^{- 8 ξ} h^{2}}{2205} \frac{13}{30} e^{- 7 ξ} h^{2} - \frac{39248 e^{- 6 ξ} h^{2}}{42875} \frac{1121}{840} e^{- 5 ξ} h^{2} - \frac{212}{125} e^{- 4 ξ} h^{2} \\ \frac{113}{70} e^{- 3 ξ} h^{2} - \frac{3337003 e^{- 2 ξ} h^{2}}{4244625} \frac{8143969 e^{- ξ} h^{2}}{67914000} \\ w_{3} (ξ) = \dots \end{array}$ (2.20)

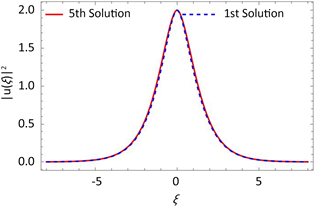
. the first and fifth order homotopy soliton solutions of the nonlinear schrödinger equation vary with $ξ$ . the parameters in the figure are selected as $α = 1, β = 2, h = - 0.3$

图1. 非线性薛定谔方程的一阶和五阶同伦孤子解随 $ξ$ 的变化。图中的参数选择 $α = 1, β = 2, h = - 0.3$

根据上式，可以逐级给出近似解，最终可通过表达式绘出图1，这里给出了一阶和五阶近似解，可以发现，方法非常有效，对于这个孤子解的形式，一阶和五阶的差别很小。

. the error between the exact solution and the fifth order homotopy approximation solution

图2. 精确解和五阶同伦近似解的误差

同样，我们也在图2给出了精确解和五阶同伦分析解的对比，不难看出，最大误差不到0.2%，我们的方法所给出的近似解可以很快收敛到精确解，说明同伦分析法能较好应用于求解此类方程，这验证了我们方法的可用和高效性。并且，这里只使用一个收敛参数h，就很好的保证了近似解的收敛性。从图2还可以看出，当变量 $ξ$ 在0以及比较大的数值时，方程的解析解和我们的近似解数值完全相同，而只有在0附近出现些许和解析解的偏离，这在计算中是需要注意的。

3. 带有高阶色散和高次非线性的薛定谔方程求解

一般情况下，介质的折射率可写成介质的线性折射率和各种原因引起的微扰和，当介质横向非均匀引起折射率分布和非线性引起的非线性折射率，折射率会发生变化。求解如下一个含四阶色散(或频散)和五次非线性的薛定谔方程

$i \frac{\partial u}{\partial t} - \frac{β_{2}}{2} \frac{\partial^{2} u}{\partial x^{2}} γ_{1} {| u |}^{2} u - i \frac{β_{3}}{6} \frac{\partial^{3} u}{\partial x^{3}} \frac{β_{4}}{24} \frac{\partial^{4} u}{\partial x^{4}} - γ_{2} {| u |}^{4} u = 0$ (3.1)

其中 $β_{2}$ ， $β_{3}$ 和 $β_{4}$ 分别代表不同阶数的色散系数， $γ_{1}$ 和 $γ_{2}$ 分别为三次和五次非线性项系数。u表示归一化的光波电场强度复振幅的包络，x和t表示严传输方向归一化距离和时间。类似地，行波变换后得到一组v和w的耦合方程组如下

$\begin{array}{l} \frac{\partial v}{\partial x} - \frac{β_{2}}{2} \frac{\partial^{2} w}{\partial t^{2}} - \frac{β_{3}}{6} \frac{\partial^{3} v}{\partial t^{3}} \frac{β_{4}}{24} \frac{\partial^{4} w}{\partial t^{4}} γ_{1} (v^{2} w^{2}) w - γ_{2} {(v^{2} w^{2})}^{2} w = 0 \\ - \frac{\partial w}{\partial x} - \frac{β_{2}}{2} \frac{\partial^{2} v}{\partial t^{2}} \frac{β_{3}}{6} \frac{\partial^{3} v}{\partial t^{3}} - \frac{β_{4}}{24} \frac{\partial^{4} v}{\partial t^{4}} γ_{1} (v^{2} w^{2}) v - γ_{2} {(v^{2} w^{2})}^{2} v = 0 \end{array}$ (3.2)

假设高阶近似解有形式

$\begin{array}{l} ϕ_{1} (ξ; q) = v_{0} (ξ) \sum_{m = 1}^{\infty} v_{m} (ξ) q^{m} \\ ϕ_{2} (ξ; q) = w_{0} (ξ) \sum_{m = 1}^{\infty} w_{m} (ξ) q^{m} \end{array}$ (3.3)

接着定义非线性算子，形式如下

$\begin{matrix} n_{v} [ϕ_{i} (ξ; q)] = - c \frac{\partial ϕ_{1} (ξ; q)}{\partial ξ} - \frac{β_{2}}{2} \frac{\partial^{2} ϕ_{2} (ξ; q)}{\partial ξ^{2}} - \frac{β_{3}}{6} \frac{\partial^{3} ϕ_{1} (ξ; q)}{\partial ξ^{3}} \frac{β_{4}}{24} \frac{\partial^{4} ϕ_{2} (ξ; q)}{\partial ξ^{4}} \\ γ_{1} (ϕ_{1}^{2} ϕ_{2}^{2}) ϕ_{2} - γ_{2} {(ϕ_{1}^{2} ϕ^{2})}^{2} ϕ_{2} \end{matrix}$ (3.4)

$\begin{matrix} n_{w} [ϕ_{i} (ξ; q)] = c \frac{\partial ϕ_{2} (ξ; q)}{\partial ξ} - \frac{β_{2}}{2} \frac{\partial^{2} ϕ_{1} (ξ; q)}{\partial ξ^{2}} \frac{β_{3}}{6} \frac{\partial^{3} ϕ_{2} (ξ; q)}{\partial ξ^{3}} - \frac{β_{4}}{24} \frac{\partial^{4} ϕ_{1} (ξ; q)}{\partial ξ^{4}} \\ γ_{1} (ϕ_{1}^{2} ϕ_{2}^{2}) ϕ_{1} - γ_{2} {(ϕ_{1}^{2} ϕ^{2})}^{2} ϕ_{1} \end{matrix}$ (3.5)

构造零阶形变方程

$\begin{array}{l} (1 - q) l [ϕ_{1} (ξ; q) - v_{0} (ξ)] = q h h n_{v} [ϕ_{1} (ξ; q), q] \\ (1 - q) l [ϕ_{2} (ξ; q) - w_{0} (ξ)] = q h h n_{w} [ϕ_{2} (ξ; q), q] \end{array}$ (3.6)

可见当q从0变化到1时，在式(3.11)可以看到 $ϕ_{1} (ξ; q)$ 和 $ϕ_{2} (ξ; q)$ 从初始猜测解 $v_{0} (ξ)$ 和 $w_{0} (ξ)$ 连续变化为原方程的解 $v (ξ)$ 和 $w (ξ)$ ，同时运用泰勒展开对 $v (ξ)$ 和 $w (ξ)$ 在 $q = 1$ 进行展开，得到级数解

$\begin{array}{l} v (ξ) = v_{0} (ξ) \sum_{m = 1}^{\infty} v_{m} (ξ) \\ w (ξ) = w_{0} (ξ) \sum_{m = 1}^{\infty} w_{m} (ξ) \end{array}$ (3.7)

两边对q求导m次同时除以 $m!$ ，再令 $q = 0$ 就能得到与零阶形变方程对应的m阶形变方程

$\begin{array}{l} l [v_{m} (ξ) - x_{m}] v_{m - 1} (ξ) = h r_{m} (v_{m - 1}) \\ l [w_{m} (ξ) - x_{m}] w_{m - 1} (ξ) = h r_{m} (w_{m - 1}) \end{array}$ (3.8)

根据 $r_{m}$ 的表达式，进而可以得到v和w的逐级近似解。下面以孤子解和周期解为例给出过程。

4. 孤子解的获得

根据孤子解特性，选择初始猜测解形式为

$v_{0} (ξ) = 2 e^{- ξ} - e^{- 2 ξ}, w_{0} (ξ) = 2 e^{- ξ} - e^{- 2 ξ}$ (4.1)

然后选择辅助线性算子

$l_{v} = \frac{\partial^{2} v}{\partial ξ^{2}} \frac{\partial v}{\partial ξ}, l_{w} = \frac{\partial^{2} w}{\partial ξ^{2}} \frac{\partial w}{\partial ξ}$ (4.2)

此时辅助线性算子有

$l [e^{- ξ} e^{ξ}] = 0$ (4.3)

依照规律可以得到

$\begin{array}{l} r_{m} (v_{m - 1}) = - \sum_{j = 0}^{i} c_{i - j} \frac{\partial v_{m - 1}}{\partial ξ} - \frac{β_{2}}{2} \frac{\partial^{2} w_{m - 1}}{\partial ξ^{2}} - \frac{β_{3}}{6} \frac{\partial^{3} v_{m - 1}}{\partial ξ^{3}} \frac{β_{4}}{24} \frac{\partial^{4} w_{m - 1}}{\partial ξ^{4}} \\ γ_{1} \sum_{i = 0}^{m - 1} w_{m - 1 - i} (\sum_{j = 0}^{i} v_{j} v_{i - j} \sum_{j = 0}^{i} w_{j} w_{i - j}) - γ_{2} \sum_{i = 0}^{m - 1} w_{m - 1 - i} (\sum_{j = 0}^{i} v_{j} v_{i - j} \sum_{j = 0}^{i} v_{j} v_{i - j} \\ \sum_{j = 0}^{i} w_{j} w_{i - j} \sum_{j = 0}^{i} w_{j} w_{i - j} 2 \sum_{j = 0}^{i} v_{j} v_{i - j} \sum_{j = 0}^{i} w_{j} w_{i - j}) \\ r_{m} (w_{m - 1}) = \sum_{j = 0}^{i} c_{i - j} \frac{\partial w_{m - 1}}{\partial ξ} \frac{β_{2}}{2} \frac{\partial^{2} v_{m - 1}}{\partial ξ^{2}} - \frac{β_{3}}{6} \frac{\partial^{3} w_{m - 1}}{\partial ξ^{3}} - \frac{β_{4}}{24} \frac{\partial^{4} v_{m - 1}}{\partial ξ^{4}} \\ γ_{1} \sum_{i = 0}^{m - 1} v_{m - 1 - i} (\sum_{j = 0}^{i} v_{j} v_{i - j} \sum_{j = 0}^{i} w_{j} w_{i - j}) - γ_{2} \sum_{i = 0}^{m - 1} v_{m - 1 - i} (\sum_{j = 0}^{i} v_{j} v_{i - j} \sum_{j = 0}^{i} v_{j} v_{i - j} \\ \sum_{j = 0}^{i} w_{j} w_{i - j} \sum_{j = 0}^{i} w_{j} w_{i - j} 2 \sum_{j = 0}^{i} v_{j} v_{i - j} \sum_{j = 0}^{i} w_{j} w_{i - j}) \end{array}$ (4.4)

接着，可以利用微分方程的解的性质，求解所需的未知参数。

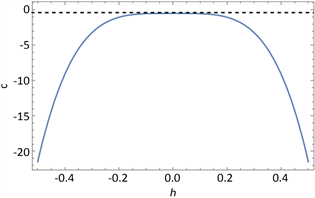
. curve of change of parameter c varying with convergence parameter h

图3. 参数c随收敛参数h的变化曲线

我们知道，微分方程的解可表达为

$\begin{array}{l} v_{m} (ξ) = x_{m} v_{m - 1} (ξ) v_{m}^{*} k_{0} e^{- ξ} k_{1} e^{ξ} \\ w_{m} (ξ) = x_{m} w_{m - 1} (ξ) w_{m}^{*} k_{0} e^{- ξ} k_{1} e^{ξ} \end{array}$ (4.5)

依据微分方程解的性质可以得到解的形式，依据同样的步骤，通过累加求和的形式，得到高阶同伦近似解 $v (ξ)$ 和 $w (ξ)$ 以及未知参数。求解高次薛定谔方程，得到未知参数c关于收敛参数h的图像如图3所示。

从图3看出，当h在0附近的一个小区间内，可保证参数c值稳定，在此区间高阶同伦解是收敛的，我们通过迭代得到高阶近似解 $v (ξ)$ 和 $w (ξ)$ 如下

$\begin{array}{l} v_{1} (ξ) = - e^{- 2 ξ} 2 e^{- ξ} - \frac{2}{99} e^{- 10 ξ} h \frac{1}{4} e^{- 9 ξ} h - \frac{80}{63} e^{- 8 ξ} h \frac{10}{3} e^{- 7 ξ} h - \frac{158}{35} e^{- 6 ξ} h \\ \frac{13}{6} e^{- 5 ξ} h \frac{8}{5} e^{- 4 ξ} h - 2 e^{- 3 ξ} h \frac{608 e^{- 2 ξ} h}{3465} \frac{773 e^{- ξ} h}{2772} \\ v_{2} (ξ) = \dots \end{array}$ (4.6)

以及

$\begin{array}{l} w_{1} (ξ) = - e^{- 2 ξ} 2 e^{- ξ} \frac{2}{99} e^{- 10 ξ} h - \frac{1}{4} e^{- 9 ξ} h \frac{80}{63} e^{- 8 ξ} h - \frac{10}{3} e^{- 7 ξ} h \frac{158}{35} e^{- 6 ξ} h \\ - \frac{13}{6} e^{- 5 ξ} h - \frac{8}{5} e^{- 4 ξ} h 2 e^{- 3 ξ} h - \frac{608 e^{- 2 ξ} h}{3465} - \frac{773 e^{- ξ} h}{2772} \\ w_{2} (ξ) = \dots \end{array}$ (4.7)

根据图3及计算，取 $h = 0.01$ ，画出孤子解图4。

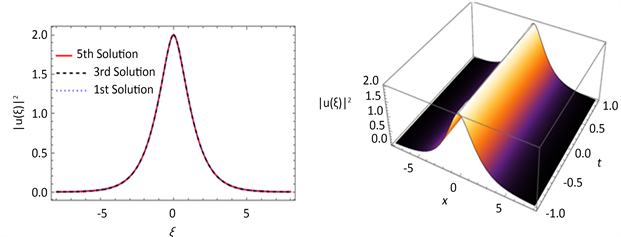(a) (b)

. (a) the evolution curves of the first, third, and fifth order homotopy soliton solutions with respect to $ξ$ . (b) the 3d plot of the fifth order homotopy approximation solution with respect to x and t. the parameters are selected as $γ_{1} = 2, γ_{2} = 1, β_{2} = 1, β_{3} = 1, β_{4} = 1, h = 0.01$

图4. (a) 一阶、三阶和五阶同伦孤子解随 $ξ$ 的演化曲线。(b) 五阶同伦近似解随x和t的变化关系3d图。参数的选取为 $γ_{1} = 2, γ_{2} = 1, β_{2} = 1, β_{3} = 1, β_{4} = 1, h = 0.01$

通过图4可以发现，一、三和五阶的近似解非常接近，说明这个方法的收敛性质非常好，仅需要计算初始几阶即可得到准确率很高的结论。

5. 周期解的获得

考虑周期解的形式为三角函数形式，选择初始猜测解为

$v_{0} (ξ) = \cos (ξ), w_{0} (ξ) = \cos (ξ)$ (5.1)

根据同伦分析可以得到

$\begin{array}{l} r_{m} (v_{m - 1}) = - \sum_{j = 0}^{i} c_{i - j} \frac{\partial v_{m - 1}}{\partial ξ} - \frac{β_{2}}{2} \frac{\partial^{2} w_{m - 1}}{\partial ξ^{2}} \frac{β_{3}}{6} \frac{\partial^{3} v_{m - 1}}{\partial ξ^{3}} \frac{β_{4}}{24} \frac{\partial^{4} w_{m - 1}}{\partial ξ^{4}} \\ γ_{1} \sum_{i = 0}^{m - 1} w_{m - 1 - i} (\sum_{j = 0}^{i} v_{j} v_{i - j} \sum_{j = 0}^{i} w_{j} w_{i - j}) - γ_{2} \sum_{i = 0}^{m - 1} w_{m - 1 - i} (\sum_{j = 0}^{i} v_{j} v_{i - j} \sum_{j = 0}^{i} v_{j} v_{i - j} \\ \sum_{j = 0}^{i} w_{j} w_{i - j} \sum_{j = 0}^{i} w_{j} w_{i - j} 2 \sum_{j = 0}^{i} v_{j} v_{i - j} \sum_{j = 0}^{i} w_{j} w_{i - j} \\ r_{m} (w_{m - 1}) = \sum_{j = 0}^{i} c_{i - j} \frac{\partial w_{m - 1}}{\partial ξ} \frac{β_{2}}{2} \frac{\partial^{2} v_{m - 1}}{\partial ξ^{2}} - \frac{β_{3}}{6} \frac{\partial^{3} w_{m - 1}}{\partial ξ^{3}} - \frac{β_{4}}{24} \frac{\partial^{4} v_{m - 1}}{\partial ξ^{4}} \\ γ_{1} \sum_{i = 0}^{m - 1} w_{m - 1 - i} (\sum_{j = 0}^{i} v_{j} v_{i - j} \sum_{j = 0}^{i} w_{j} w_{i - j}) γ_{2} \sum_{i = 0}^{m - 1} w_{m - 1 - i} (\sum_{j = 0}^{i} v_{j} v_{i - j} \sum_{j = 0}^{i} v_{j} v_{i - j} \\ \sum_{j = 0}^{i} w_{j} w_{i - j} \sum_{j = 0}^{i} w_{j} w_{i - j} 2 \sum_{j = 0}^{i} v_{j} v_{i - j} \sum_{j = 0}^{i} w_{j} w_{i - j}) \end{array}$ (5.2)

和图3类似，得到未知参数c关于收敛参数h的图像如下图5所示。

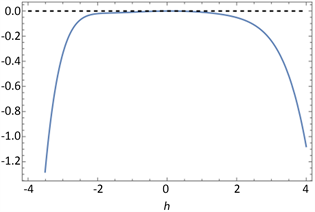
. curve of parameter c evolves with h

图5. 参数c随收敛参数h的变化曲线

$\begin{array}{l} \begin{matrix} v_{1} (ξ) = \cos (ξ) \frac{1}{64} h \cos (3 ξ) \frac{1}{192} h \cos (5 ξ) \\ h [\frac{1}{8} \cos (3 ξ) \frac{1}{8} {(- \cos (3 ξ) - \cos (5 ξ))}^{2} \frac{1}{8} \cos (5 ξ)] \\ - h \cos (ξ) [\frac{1}{8} \cos (3 ξ) \frac{1}{8} {(- \cos (3 ξ) - \cos (5 ξ))}^{2} \frac{1}{8} \cos (5 ξ) \frac{1}{48}] \end{matrix} \\ v_{2} (ξ) = \dots \end{array}$ (5.3)

$\begin{array}{l} \begin{matrix} w_{1} (ξ) = \cos (ξ) - \frac{1}{64} h \cos (3 ξ) - \frac{1}{192} h \cos (5 ξ) \\ h [- \frac{1}{8} \cos (3 ξ) - \frac{1}{8} \cos (5 ξ) \frac{1}{8} {(\cos (3 ξ) \cos (5 ξ))}^{2}] \\ - h \cos (ξ) [- \frac{1}{8} \cos (3 ξ) - \frac{1}{8} \cos (5 ξ) \frac{1}{8} {(\cos (3 ξ) \cos (5 ξ))}^{2} - \frac{1}{48}] \end{matrix} \\ w_{2} (ξ) = \dots \end{array}$ (5.4)

根据图5以及计算，发现参数c随h的变化在一个小范围内是平直的，我们可取 $h = 0.1$ ，进而给出周期解图6。

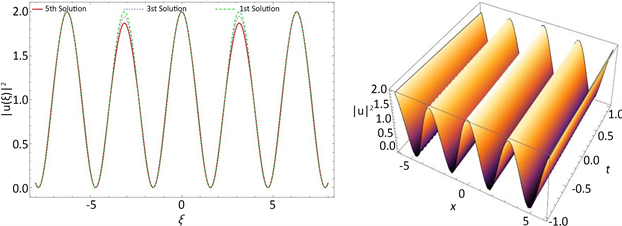(a) (b)

图6. (a) 一阶、三阶和五阶同伦周期解随 $ξ$ 变化曲线。(b) 五阶同伦周期解随x和t的变化关系3d图。参数的选取为 $γ_{1} = 2, γ_{2} = 1, β_{2} = 1, β_{3} = 1, β_{4} = 1, h = 0.1$

通过图6发现，一阶到五阶的解随着振荡出现部分偏离，一阶解随 $ξ$ 的变化幅度基本不变，而通过更高阶的计算，我们发现，三阶和五阶曲线在从 $ξ = 0$ 往正负开始计数的偶次振荡逐渐偏离一阶解的曲线，迭代次数越多，偏离一阶解越明显。说明在周期解的情况下，我们的同伦分析方法依然可以在比较小的迭代次数之后，得到准确度高的解，但是一阶解和高次迭代的解逐渐出现部分偏离，这里有规律的偏离也恰好体现了方程解的内禀对称性。

6. 结论

本文通过对同伦分析法的介绍，研究了非线性薛定谔方程的解。对具有高阶色散和高次非线性的非线性薛定谔方程进行了研究，通过将原始的复系数方程变成一组实系数方程，然后进行求解，讨论了方程的孤子解和周期解。这些解在数学和相关领域的应用中是广受关注的，也具有很强的实际应用背景。通过绘制收敛参数h的曲线，可以得到参数的取值范围进而给出方程的解中各参数的取值范围。需要指出的是，这里的求解过程不依赖于方程中含有小参数，因此这个方法在应用于求解非线性偏微分方程中具有优势。可以发现，无论是孤子解还是周期解，随着迭代次数的增加，可以更加逼近真实解的情况，这提示我们，有关方法及其应用可以给相关的研究提供有益参考。

基金项目

本文受到国家自然科学基金项目号11804396的资助。

参考文献

[1]	debnath, l. (2005) nonlinear partial differential equations for scientists and engineers. 2nd edition, birkhäuser, boston.
[2]	周国全, 雒润嘉, 齐蓥. 基于hirota方法探求非零边界条件下mnls/dnls方程的孤子解[j]. 物理与工程, 2023, 33(4): 79-84.
[3]	毛辉. 两个广义短脉冲方程的bäcklund变换及其应用[j]. 应用数学学报, 2021, 44(3): 340-354.
[4]	adomian, g. (1988) nonlinear stochastic systems theory and applications to physics. springer science & business media, dordrecht.
[5]	clarkson, p.a. and kruskal, m.d. (1989) new similarity reductions of the boussinesq equation. journal of mathematical physics, 30, 2201-2213.
[6]	lou, s.y. and ma, h.c. (2005) non-lie symmetry groups of (2 1)-dimensional nonlinear systems obtained from a simple direct method. journal of physics a: mathematical and general, 38, l129.
[7]	wu, x.h., gao, y.t., yu, x., et al. (2022) modified generalized darboux transformation and solitons for a lakshmanan-porsezian-daniel equation. chaos, solitons & fractals, 162, article id: 112399.
[8]	yong, x., wang, h. and gao, j. (2014) integrability and exact solutions of the nonautonomous mixed mkdv-sinh-gordon equation. communications in nonlinear science and numerical simulation, 19, 2234-2244.
[9]	wu, j. (2022) wronskian and grammian conditions, and pfaffianization of an extended (3 1)-dimensional jimbo-miwa equation. mathematics and computers in simulation, 198, 446-454.
[10]	aslan, i. (2010) a note on the (g’/g)-expansion method again. applied mathematics and computation, 217, 937-938.
[11]	ebadi, g. and biswas, a. (2016) application of g’/g-expansion method to kuramoto-sivashinsky equation. acta mathematicae applicatae sinica, english series, 32, 623-630.
[12]	nuseir, a.s. and al-hasson, a. (2012) power series solution for nonlinear system of partial differential equations. applied mathematical sciences, 6, 5147-5159.
[13]	赵嘉, 乔雨. 经典lie-yamaguti yang-baxter方程和lie-yamaguti双代数[j]. 中国科学(数学), 2023, 53(10): 1303-1324.
[14]	王贵贤, 王秀彬, 韩波. 聚焦kundu-eckhaus方程的反散射变换法:阶跃振荡背景下的长时间渐进性[j]. 数学物理学报, 2023, 43(4): 1085-1122.
[15]	wang, m., zhou, y. and li, z. (1996) application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics. physics letters a, 216, 67-75.
[16]	liao, s. (2003) beyond perturbation: introduction to the homotopy analysis method. crc press, boca raton.
[17]	liao, s. (2009) notes on the homotopy analysis method: some definitions and theorems. communications in nonlinear science and numerical simulation, 14, 983-997.
[18]	liao, s. (2012) homotopy analysis method in nonlinear dif-ferential equations. higher education press, beijing.
[19]	abbasbandy, s. (2006) the application of homotopy analysis method to nonlinear equations arising in heat transfer. physics letters a, 360, 109-113.
[20]	hashim, i., abdulaziz, o. and momani, s. (2009) homotopy analysis method for fractional ivps. communications in nonlinear science and numerical simulation, 14, 674-684.
[21]	naik, p.a., zu, j. and ghoreishi, m. (2020) estimating the ap-proximate analytical solution of hiv viral dynamic model by using homotopy analysis method. chaos, solitons & fractals, 131, article id: 109500.
[22]	周杰, 常学平, 李映辉, 等. 基于同伦分析法的fgm输流管非线性频率分析[j]. 应用数学和力学, 2023, 44(2): 191-200.
[23]	wang, j., li, b. and ye, w. (2010) approximate solution for the klein gordon-schroedinger equation by the homotopy analysis method. chinese physics b, 19, 87-93.

为你推荐

凯发娱乐官网的友情链接