1. 引言
作为一种开创性的量子模型,一维(1d) hubbard模型 [1] 已被广泛用于描述低维多体系统中的电子关联。hubbard模型构成了我们理解高度相关材料丰富物理的基础,然而,它的标准哈密顿量仅包括与占据无关的跳跃(t)和在所有位置的等位相互作用(u)。通常,从一个位点到另一个位点的跳跃与这两个位点的电子占有数有关,这导致了密度相关的跳跃 [2] [3] [4] 的发生,它描述了位于位点和键上的电荷之间的相互作用,也称为键–电荷相互作用(x) [5] [6] [7] [8] 。u项和x项是通过关注两体势的矩阵元素的不同选择,从相同的紧束缚模型哈密顿量 [1] 中获得的。通过利用wannier态
,
,
。在位置表示中,u项和x项分别对应于势的对角矩阵元素和非对角矩阵元素。一开始,键–电荷相互作用被引导来解释混合价态材料的低能物理 [9] 。随后,x相互作用在不同的背景下得到了广泛的研究 [10] - [16] 。特别是,一维t-u-x模型 [17] [18] [19] [20] [21] 的相图研究受到了相当大的关注,其哈密顿量的形式为 [17]
(1)
通过产生(
)和湮灭算符(
),可得到数密度算符
。u项描述局域电子,x项延伸到涉及最近电子的非局域轨道。此外,在一些络合物中,x的值可能更大 [22] 。系统(1)的基态性质引起了人们的极大兴趣。在半填充时,aligia等人展示了一种非常规的绝缘体–超导体转变 [17] 。buzatu展示了在半填充时,系统不受x项的影响,其特征是自旋密度波(sdw)相,而在非半填充时x和u相互作用相互竞争,导致基态变成具有几种类型不稳定性的金属相 [18] 。
hubbard模型被视为相关系统的原型,并解释了许多材料的性质,而这些性质并没有用平均场理论来解释。相比之下,t-u-x模型可以描述一系列更多的现象。此外,具有格点间扩展的对角相互作用,
,也被广泛研究 [23] - [30] 。最普遍的扩展是由bks哈密顿量给出的,它考虑了所有可能的最近邻耦合 [31] 。尽管如此,这些模型还是假设任何晶格位点都具有相同的在位相互作用。我们不得不承认,这个方案既简化了复杂的相互作用,又突出了物理性质。然而,在一些材料中确实存在不同的hubbard相互作用,如high-tc la2cuo4,其中cu和o位点具有不相等的在位排斥作用 [32] 。emery进一步将cu-o平面转化为1d模型 [33] 。japarized等人通过使用cu-o链的1d哈密顿量研究了hubbard相互作用的不等价性 [34] 。在本文中,我们扩展了模型(1),在释放等hubbard能量假说的基础上,选取了奇数和偶数晶格位点上不同的现场相互作用,分别为uo和ue。考虑到这一点,该模型可以用哈密顿描述如下:
(2)
在位排斥影响umkalpp散射过程中,人们普遍认为,在1d标准情况下(
),这种散射仅发生在半填充时。
(
)的作用是有利于(阻碍)带有非零电荷的位点的跳跃 [8] 。在此,我们重点讨论四分之一填充,且所有参数均为正值(
)。我们只考虑弱耦合的情况,在这种情况下,玻色化和重正化群分析方法可以有效地应用。结果表明,当uo和ue都大于
时,就会出现umklapp过程。这一特征在一维传统t-u-x模型(1)中是没有的。量子相图包含一个具有单线超导(ss)不稳定性的金属相和两个具有自旋密度波(sdw)和电荷密度波(cdw)不稳定性的绝缘相。
2. 玻色化和重整化群分析
费米系统的低能特性主要取决于费米表面附近的态。在一维情况下,我们只需考虑费米点附近的激发。在这种情况下,晶格场算符可以用左移(
)和右移(
)分量展开为 [35] ,
(3)
其中,j位点的平均电子填充度定义为
,n电子平均占据n0个位点。一维电子系统具有电荷–自旋分离的特性。umklapp和后向过程分别影响电荷和自旋激发。相关的umklapp散射会产生能隙,从而导致绝缘态。相反,不相关的过程不能产生间隙,系统就是导体。同样,后向散射的相关性也决定了自旋间隙的存在。为了突出模型(2)不同于模型(1)的量子特性,我们分析了交替hubbard相互作用对umklapp过程的影响。为此,我们将哈密顿方程(2)中的uo和ue项重写为另一种等价形式
(4)
通过表达式(3),上述均匀项和交替在位作用项被转化为手性场的组合
(5)
(6)
这里
和
。(5)和(6)中携带振荡因子的最后一项描述了我们最关心的umklapp过程。显然,只有在
或1/4时,这两个项才会有区别,这表明umklapp过程要么发生在半填充时,要么发生在四分之一填充时。在连续极限中,晶格场算符可以由连续场代替:
,
。这些手性费米子算子又可以用一对对偶玻色算子
和
来表示 [35]
(7)
(8)
其中
对应于1 (−1)的值。hermitian因子
保持了不同费米子的反对易关系,
。玻色场
和
遵循
。玻色化方法 [35] [36] [37] 已被广泛应用于一维量子系统,其中的物理现象分别由自旋(
)和电荷(
)通道描述。
按照惯例,电荷–自旋耦合项在弱耦合机制中作为一个强无关算子可以省略 [38] [39] [40] [41] [42] 。在这一方法中,哈密顿(2)被转换为用独立电荷场和自旋场来表示:
(9)
和
项分别对应后向过程和umklapp过程。参数
和
的关系是
,费米速度
。自旋和电荷luttinger参数
主导着关联函数的衰变行为。g和k的振幅由相互作用和填充决定,计算公式为
(10)
(11)
(12)
(13)
除了谐振项之外,哈密顿方程(9)中还有余弦项,它们对电荷隙和自旋隙的存在与否有重要影响。这对应于已知正弦–戈登(sg)模型的重整化群(rg)分析 [35] 。根据初始g和k之间的关系,该模型的低能激发有两种不同类型的区域:
1) 对于
,rg流被限制在强耦合区域。表征后向过程或umklapp过程的余弦项变得相关,自旋或电荷扇区出现了间隙。为了最大限度地减少基态能量,当
时,
场被固定在期望值
附近;而当
时,
场固定在0周围 [39] [40] 。
2) 对于
,系统处于弱耦合区域。随着长度尺度的增大,余弦项被重正化为无关项。激发时没有间隙,并且
场不会被固定。
3. 基态相图
在本文中,我们只考虑四分之一填充。从方程(10)和(12)可以看出,存在
的关系。这在物理上来自自旋扇区中的su(2)对称性,并且流沿着rg流图的分界线的方向进行。自旋间隙在
时打开,在
时关闭。因此,自旋间隙相变发生在:
(14)
在无自旋带隙的情况下,定点取
的值。
在具有较低u(1)对称性的电荷通道中,情况变得有些复杂。电荷流偏离了分界线,有了更多的选择。根据rg分析,电荷激发在以下条件下是大质量的:
(15)
同样地,它对应于不等式关系
或
。电荷场的相应期望值为
或
。无论哪种情况,都会出现umklapp散射。
与不等式(15)相反的是
(16)
描述了弱耦合区域,在该区域内,电荷激发是无质量的。重正化流最终归零,umklapp过程消失。由此可见,电荷隙过渡的边界有两个分支。对于
,为
(17)
而在
,为
(18)
在无电荷间隙区,除了边界(17)和(18)外,不动点的特征是
。
通过了解每个扇区中的转变,现在可以确定相位区域。首先,我们排除了键位不稳定性的存在,因为它们只出现在半填充的情况下 [41] 。因此,我们只需要考虑在位密度波和超导不稳定性,相应的序参量由玻色子场定义为:
(19)
(20)
(21)
(22)
与标准情况一样,前两个参数与奇数和偶数位置无关,描述的是ss和ts相关性。而后两者描述的是sdw和cdw相关性,依赖于位置的奇偶性:在奇数位点,它们的计算公式为:
(23)
(24)
在偶数位置,它们的形式为:
(25)
(26)
通过上述分析得出了相图(图1),该相图分为五个区域,包括三个不同的相。
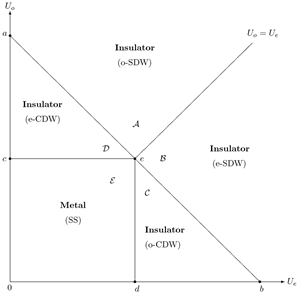
. phase diagram of the model (2) at quarter filling and at weak coupling
图1. 模型(2)在弱耦合情况下,考虑四分之一填充时的基态量子相图
在a和b的半间隙扇区中,电荷通道有间隙,而自旋通道没有间隙。这样就无法产生无电荷间隙的 和ss不稳定性,系统只能是绝缘体。在另一方面,
场是波动的,而
场是固定的,在a中赋予
,在b中赋予
。很容易发现,在a区域中,
和
取非零值,而在b区域中,非零序参量为
和
。为了确定主导序参量,我们借助于相应的关联函数(
) [23] :
,而
。显然,sdw的不稳定性抑制了cdw的不稳定性。基态处于sdw相关性占主导地位的绝缘相。我们分别称它们为a区的o-sdw和b区的e-sdw。
在c和d的全间隙扇区中,自旋和电荷激发都是间隙的。这与umklapp和后向散射有关。ts、ss和sdw不稳定性都被抑制。在c区域,
,因此只有
。在d区域,
,而
,因此只有
。该系统是一个具有o-cdw或e-cdw不稳定性的绝缘体。
在另一个半间隙扇区e中,它的激发与区域a和b中的激发相反。自旋间隙处处打开,这导致抑制了ts和sdw的不稳定性。同时,电荷间隙总是关闭的,从而导致没有umklapp过程。这与luther-emery (le)后向散射模型的结构相吻合 [42] 。另一方面,自旋场的
,而
场是波动的。因此,
和
可以同时不为零。然而,它们的相关性表现出不同的衰减行为:
,而
。由于
,基态表现出具有以ss相关性为主导的le金属特征。
4. 总结
我们研究了一维扩展hubbard模型,除了额外的键荷排斥相互作用外,在位排斥作用考虑了在奇数和偶数位置不相等的情况。相比之下,本项研究可以提供对在位电子的更一般的描述。此外,所涉及的模型还与一些实际材料有关。因此,无论是理论还是实验,我们的考虑都是必要的。通过玻色化方法,将费米子哈密顿量转化为玻色子形式,通过两个独立的自旋场和电荷场可以方便地阐明基态性质。在自旋–电荷分离的假设下,该模型的红外行为可以用sine-gordon模型来说明,并且自旋隙和电荷隙可以独立存在。与此相关的后向和umklapp过程的出现可以通过重整化群分析来实现。结果表明,在四分之一填充的情况下,不相等的哈伯德斥力对umklapp散射有关键影响,在
的情况下会发生umklapp散射。这不仅存在电荷隙转变,还存在自旋隙转变。如上图1所示:完整的相图由五个区域组成,分别包括三个不同的相。在以uo为纵坐标,ue为横坐标的平面上,相图相对于
线是对称的,这从物理角度看是一个自然的结果。由于所考虑的模型满足晶格平移不变性,当交换ue和uo参数时,哈密顿(2)保持不变。因此,无论是
还是
,基态结构必须是相同的。电荷–间隙相变线
和
,交点所围成的区域被划分为金属相和绝缘相,而自旋–间隙相变线
则把绝缘项分别划分为以cdw为主导的全隙相和以sdw为主导的半隙相。这种现象不同于传统的t-u-x模型的特点。该项研究有望增加对低维多体问题的理解。