1. 引言
自激光冷却技术出现 [1] [2] [3] [4] 以及玻色–爱因斯坦凝聚(bose-einstein condensation,简称bec)的实验室实现 [5] [6] [7] [8] [9] 以来,冷原子物理领域迅速成为量子科学研究的前沿。冷原子的温度极低,运动速度缓慢,粒子相互之间碰撞很少,同时,德布罗意波长很长,具有很强的相干性 [10] 。通过feshbach共振等技术,可以实现对冷原子系统的高度精准操作,操纵冷原子并将其作为一个理想的研究平台,用于研究各种量子系统 [11] 。数十年来,冷原子广泛活跃于量子通信、量子计算与量子模拟、量子精密测量等新兴领域,是人们从宏观世界中理解微观量子世界,并从微观量子世界过渡到宏观世界很好的研究途径 [12] 。
旋转量子气体的研究是极其引人注目的,在旋转框架下观察冷原子云团的行为,在近现代几乎所有物理研究领域都有着重要的作用。从核物理,气象物理,到海洋物理,甚至在黑洞、恒星及宇宙的形成中,旋转量子气体的研究给了一个友好的模型框架,给科学家们去探索广袤的宇宙和微渺的粒子世界敞开了一扇大门。近几年,冷原子领域一直有人不断尝试通过使用不带电荷的中性原子来模拟磁场中的二维电子气体,以实现玻色版本的量子霍尔效应和观测物质的非阿贝尔相。其中,来自麻省理工学院的richard fletcher等人在2021年的实验上成功实现了这种想法 [13] 。小组成员通过压缩几何量子不确定性,成功地将bec旋转,并将其限制在最低朗道能级(lowest landau level,简称lll)中,通过调整转速和相互作用强度来模拟和调控强关联玻色流体的行为。随后,该小组进一步在朗道规范下研究纯粹相互作用驱动的动力学问题。通过将一百万个钠原子冷却到十亿分之一开尔文,并将其限制在特定的旋转规范势阱中,从凝聚物中观察到奇妙的量子龙卷风暴,并随之成功预测出量子霍尔结晶的出现 [14] 。
可以确切地说,旋转量子气体的研究为玻色–爱因斯坦凝聚与量子霍尔效应之间的研究架起了桥梁,本文以超冷玻色气体为研究主体,尝试着去理解和窥探相互作用和旋转下的粒子在量子世界里的各种行为。考虑将粒子云团绕z轴旋转,通过高而扁平的三维谐振势场,使粒子进一步只在z = 0处活动,这样我们只需研究二维体系,可以得到二维形式的有效哈密顿量。进一步求解这个哈密顿方程,系统基态和激发态的很多信息可以被发掘。在这个极尽深寒的量子世界里,可以发现,旋转在形式上等效于磁场的作用,由磁场的洛伦兹力更迭为径向的科里奥利力。力的作用使得自由粒子的状态被重构为更为离散并高度简并的朗道能级,对于低能情况,通过最低能级构造波函数同样可以描述我们的体系。当然,系统的性质对粒子间的相互作用异常敏感,在较弱的相互作用下,这时的系统是纯粹的玻色爱因斯坦凝聚,所有粒子全都占据在单粒子能量最低处,随着相互作用增加出现一定的激发,导致量子涡旋的出现并形成具有周期结构的涡旋阵列。同时,旋转速度的变化,也会影响涡旋的大小和密度。
2. 模型提出
2.1. 有效哈密顿量和二维gross-pitaevskii方程
考虑粒子在三维各向同性的谐振势阱中,其沿oxy平面和沿z方向的谐振频率分别为
和
,粒子的有效质量为
,受到沿z方向角频率
的旋转平台作用。因此,单体哈密顿量可以描述为
(1)
这里,角动量算符
。在本文构造的旋转框架里,旋转轴为z轴,借助z分量的向量三重积公式:
,等效的矢势(
)和场强
之间的关系进一步可以表述为
(2)
然后利用标量四倍积公式,得到
(3)
因此单体哈密顿量可以进一步整理为
(4)
为了忽略上式中的第二项,考虑离心力极限 [15] :
,哈密顿量则可以进一步改写为
(5)
接下来,扩展到考虑相互作用项的多体哈密顿量。基于hartree近似和赝势模型假定 [16] ,可以认为所有的全同粒子都处在相同的单体波函数状态下,系统的波函数通过单体波函数乘积的方式表示,而粒子与粒子之间的相互作用,假设所有的粒子之间都处在很短的力程之内,受到相同大小的力的作用,可以借助平均场耦合常数,用虚构的赝势取代实际相互作用势场。考虑二次量子化形式表述,通过玻色场算符
,描述两体相互作用的哈密顿量可以写成动能项和相互作用项相加的形式
(6)
这里,两体相互作用通过赝势给出
。其中,
,
,
是相互作用强度,或者称之为三维空间平均场耦合常数,且
表示s波散射长度。
是狄拉克delta函数,其值在原点处为无限大,在其它点为零,并满足空间积分归一化。利用狄拉克delta函数的性质,哈密顿量(6)的相互作用部分可以重写为
(7)
因此,系统的波函数随时间的演化满足gross-pitaevskii方程
(8)
考虑不含时的稳态形式,取
,方程(8)则变为
(9)
同时,如果将研究聚焦于oxy平面上,对z方向施加严格的限制,考虑高且平坦的谐振子势,满足
。三维空间波函数就可以用二维平面波函数表示
(10)
这里,
是特征长度。将波函数(10)带入方程(9)中,重新整理可以得到二维平均场耦合常数
和二维化学势
。最终,比对三维形式可以得到相应二维形式的有效哈密顿量
(11)
和二维gross-pitaevskii方程
(12)
2.2. 规范选取与无量纲化处理
显然,方程(2)中的规范势
满足规范不变性,
,对不同的规范势选取
,仅增加或减小规范势相位的梯度,其本身的物理性质并不会改变。为了寻找本征函数,需要明确具体规范势的选取,当然这种选取不是唯一的,这里仅考虑两种不同的规范选取 [17] 。
一种是朗道规范,规范势可取
(13)
这里,
是回旋频率。特别地,选取朗道规范(13)后,将破缺x方向的平移不变性和旋转不变性,但y方向还具有平移不变性。
另一种是对称性规范,规范势可取
(14)
与朗道规范(13)的选取不同的是,对称性规范破缺了x方向和y方向的平移对称性,保留了oxy平面上旋转对称性。
为了方便后续的数值计算及展示结果,考虑无量纲化处理,借助特征长度
,取
,
,
,
,
,两边同时除以能量单位
。同时,忽略新的无量纲的量上的“~”,得到的新的变量是不包含单位的无量纲数。
3. 模型求解
在本文中,仅考虑朗道规范势
,此时冷原子云团就像只在y方向流动的流体。在附录中,给出单体朗道规范波函数可由y方向的平面波函数与x方向的谐振子的本征函数
(15)
这里,
是关于位置x上的厄米多项式。特别地,定义一个与厄米多项式 [18] 有关的函数
(16)
其满足规格化条件
(17)
因此场算符可用相应的单体朗道规范波函数作为基展开
(18)
这里,
是状态
的湮灭算符。对于低能系统,可以忽略较高的朗道能级,仅仅使用lll展开是合理的,且可以大大降低计算的复杂程度。因此,单体朗道规范波函数可以进一步表示为
(19)
将新的展开形式(19)应用到方程(11)中,同时对全空间积分,这时得到仅含
自由度的一维哈密顿量
(20)
这里,
。采用不同
自由度下朗道规范波函数态叠加来定义波函数 [18]
(21)
这里,
是选取
格点总数,称之为组分数 [19] ,ii是序号。
是对应选取子波函数的系数,为复数,定义一个归一化的系数f,满足
(22)
是相应的相位因子。接着定义
(23)
因此能量可以给出
(24)
这里,
,
,
,
,
,约定
,相互作用系数
。固定n的情况下,可以在上述定
义域中寻找e的最小值解emin,从而获得系统的基态波函数和基态能量。
4. 结果分析
首先,我们研究组分数以及凝聚分数与相互作用之间的关系。表1为通过求解emin确定的波函数叠加系数和相位因子以及其它详细的数据,通过这些数据可以得到相应下体系的基态波函数和基态能量,当然,我们仅仅罗列了关键节点的数据。图1给出了组分数与凝聚分数随相互作用系数
的变化,从0增加到1.23、1.36和4.92,组分数也随之从单组分变化为三组分,然后是两组分,最后又变为三组分。在0~1.23区域,凝聚分数恒为1,粒子完全凝聚在最低能态上,表现为单组分,是典型的玻色爱因斯坦凝聚,我们将此区域记为s1区。对于1.23~1.36区域,凝聚分数随相互作用系数从1开始逐渐线性降低,但粒子绝大多数仍然凝聚在
处,只有少部分被激发,在逼近1.36处凝聚分数约为0.92,记为s2区域。到了1.36~4.92区域,凝聚分数则是恒定为0,粒子由少部分被激发突变成完全被激发,记为s3区域。对于大于4.92区域,凝聚分数随
逐渐降低,此时凝聚分数完全激发退回到部分激发,和s2的情况不同的是,激发是相对充分的,此区域凝聚分数均小于s2区域,且随
的增加逐渐下降。图2给出各区域边界系统的能量最小值与kc的分布关系,从无相互作用开始,此时能量最小值与kc无关,如图2(a)。随着
进一步增加至1.23附近,突然变成在kc = 1.59处出现最小值,如图2(b)。随着相互作用增加kc也增加,当
越过1.35到1.36之后,如图2(c)所示,能量最小值的取值kc由1.60突变为0.92,并同样随
的增加而增加。在
附近,能量最小值处kc的取值由1.22左右变成了2.04附近。
对于系统的不同区域,密度分布与相位分布的存在明显地不同。图3(a)~(d)和图3(e)~(h)是相互作用系数
分别为1、1.3、4、10时的密度分布和相位分布图,分别对应于s1~s4区域。对s1区域而言,无论相互作用系数
如何变化,其密度分布为一条直的条纹,相位分布则恒为0。到了s2区域,密度分布从条纹状变成波浪纹状,相位分布则变成明显的“雪伽”型,相位正、负与零的交界处对应于波浪纹的凹点。同时,随
的增加密度分布中的波纹变得越来紧密。临界点可以看成一个相变点,相变的结果是产生拓扑缺陷–涡旋。涡旋的环流是量子化的,涡旋的出现可以作为体系存在超流态的判据。在s3区域中,其密度分布图中出现量子化涡旋,涡旋数目随
的增大而增加,涡旋中心之间的距离也变得越来越近,而相位分布则出现“雪伽”的交汇处。对于s4区域,密度分布中涡旋仍然存在,但涡旋列阵由一列变成两列,两列涡旋中心交替分布,同样满足随
的增大涡旋数增加,且涡旋两边的密度图随
的增加而变深。
. energy optimization (minimum value) solution result data for different interaction coefficients
表1. 不同相互作用系数
下能量最优化解(最小值)结果数据
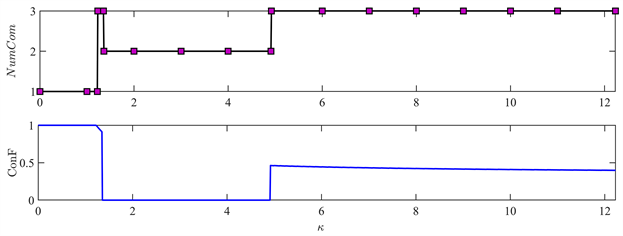
. diagram of the variation of number of component (numcom) and condensed fraction (conf) changes with interaction coefficient
图1. 组分数和凝聚分数随相互作用系数
的变化图
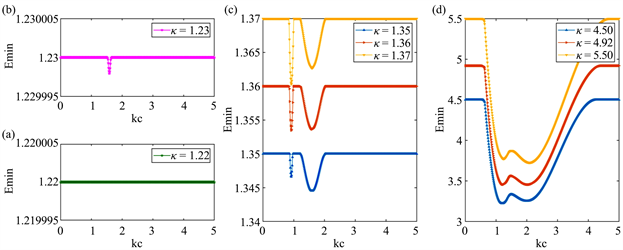
. the relationship between the minimum system energy (emin) and kc. (a)
; (b)
; (c) from bottom to top:
, 1.36, 1.37; (d) from bottom to top:
, 4.92, 5.5
图2. 系统能量最小值emin与kc的关系。(a)
;(b)
;(c) 从下到上:
、1.36、1.37;(d) 从下到上:
、4.92、5.5
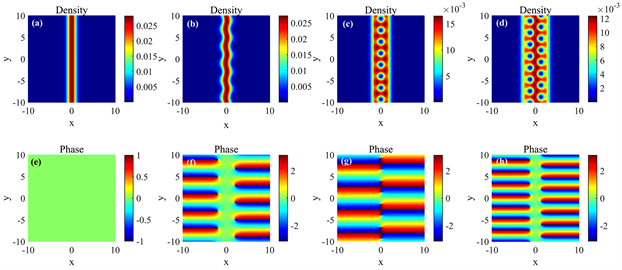
. the density distribution and the phase distribution plots under the different interaction coefficients
. density distribution: (a)
; (b)
; (b)
; (b)
; phase distribution: (e)
; (f)
; (g)
; (h)
图3. 不同相互作用系数
下的密度分布和相位分布图。密度分布:(a)
;(b)
;(b)
;(b)
;相位分布:(e)
;(f)
;(g)
;(h)
区域s2与s3间有一个重要节点,在这个点之前,粒子普遍分布在
态上,在这个点之后,无论是两组分,三组分还是更多组分,粒子将更多的被激发。根据模型求解时约定,
,因此可以将凝聚部分的态产生和湮灭算符用c-数
表示 [20] ,即:
,
是系统凝聚在
态上的粒子总数,满足
。任意的态产生和湮灭算符可以表示成凝聚和非凝聚部分的形式 [21] ,即
(25)
这里,
。在节点之前,凝聚是主要部分,而激发是小量,可将动能项和相互作用项中保留
的平方项和四次方项,忽略其它小量,哈密顿量(20)则可近似写成
(26)
这里,
,
,
。引入准粒子的产生算符
和湮灭算符d,则原粒子产生算符
和湮灭算符b与之满足bogoliubov变换 [22]
(27)
直接对角化,得到系统能量
(28)
和激发谱
(29)
其中,方程(28)中第一项e0为系统基态能量,第二项为基态能量的修正项
,第三项为准粒子激发项。基态能量e0与ky无关,与相互作用系数
呈正比,而基态能量修正项
与ky有关,随ky的分布如图4(a)所示。可以看出,对于基态来说,随着相互作用系数
增加到1.225,体系也从单组分凝聚过渡到三组分,最小值点由一个变成三个,并开始出现元激发。图4(b)是方程(23)给出的bogoliubov激发谱,当
时,开始出现旋子谱 [11] ,能谱结构与长程偶极相互作用或自旋轨道耦合的超流氦4类似 [23] [24] [25] ,激发能谱表现出从ky原点开始线性增长,这个线性区域称为声子激发。声子与原粒子显著不同,具有非常纯粹且普适的性质,其声子集合可以用来描述具有超流态系统的低能物理行为。随着ky的增长,能谱出现拐点,能量首先出现最大值,然后出现最小值。其中能量接近最大值处称为maxons,最小值处称为旋子激发,旋子是超流体出现的另一种元激发,旋子之间可以通过交换声子相互关联,从而受到相互作用在系统集体行为的支配 [26] 。在
,得到一个临界旋子点,在
处,其能量最低点与原点处值相同,对应于三组分凝聚的出现。然而,当相互作用系数
越过1.225之后,其激发能量
是复数,这样的声子激发和旋子激发都是不稳定的,系统变得更加复杂。图4(c)是给出的稳定与不稳定激发能相互作用梯度随ky的分布,在
时,这种激发的不稳定性变得愈加剧烈。最后,在
时,得到两个不稳定的goldstone分支
和
。
随着相互作用系数
继续增加,凝聚在
的部分已不在显著,bogoliubov近似方案就变得不那么适用了,需要另辟蹊径。一个可预测的趋势是组分数会变得更多,而各组分支上的粒子数分布变得更平均,因此动能项对系统的影响就会变得越来越弱,相互作用对动能项的支配地位显著逐渐提高,表现为系统趋向于晶格化,一个可被证实的结果是出现局域结晶序。同时,随着涡旋数目的增加,晶体结构周期性增强,在某些情况下平移对称性和旋转对称性都可能出现,一些强关联量子态被预测,在粒子数n和涡旋数
的一定比值下,可能存在整数和分数量子霍尔态 [27] 。这里,定义填充因子
。需要进一步说明的是,对于固定粒子总数的系统,为了获得足够多的涡旋数,这里不仅需要尽可能大的相互作用系数
,使得涡旋能填满整个给定的空间,同时,也需要足够大的旋转频率,使得特征长度
足够小,涡旋变得更小,从而出现更多的涡旋,获得更小的填充因子,甚至出现分数填充。当然,对于玻色系统,填充因子的取值可以是任意的,包括足够大或者足够小的取值。对于不同的填充的因子,基态波函数会有不同结构。这里,给出一个临界的填充因子
,其中
,其基态出现周期性三角涡旋晶格结构,如图5(a)所示。图5(b)是三角涡旋晶格结构的局部放大示意图,这里,a是晶
格常数,同时,定义涡旋阵列之间的平均间距
和
。可知,
,其中
,
,其中
,此时
。
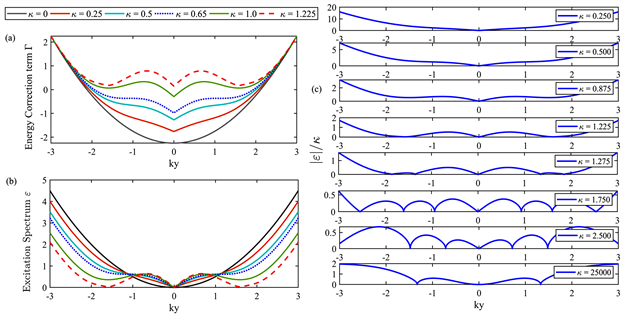
. spectral distribution. (a) the ground state energy correction term of the system is distributed with ky. (b) the excitation energy of the system is distributed with ky. (c) the potential gradient of stable and unstable excitation energy interaction varies with ky. from top to bottom,
are 0.25, 0.5, 0.875, 1.225, 1.275, 1.750, 2.5, 25000
图4. 能谱分布。(a) 系统基态能修正项随ky分布。(b) 系统激发能随ky分布。(c) 稳定和不稳定激发能相互作用势梯度随ky分布。从上到下,分别为0.25,0.5,0.875,1.225,1.275,1.750,2.5,25000
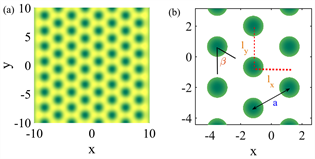
. the vortex-lattice model. (a) triangular vortex lattice. numcom: 9, kc: 2.35. (b) schematic of local amplification. scope: (−5, −5) < (x, y) < (3, 3)
图5. 涡旋晶格模型。(a) 三角涡旋晶格。numcom: 9,kc: 2.35. (b) 局部放大示意图。范围:(−5, −5) < (x, y) < (3, 3)
5. 总结
我们回顾了数值求解旋转框架下相互作用超冷玻色气体的过程,从无相互作用到相互作用系数
。主要聚焦于模拟相互作用迫使超冷玻色气体形成涡旋的过程,得到不同区域下的密度分布和相位分布,以及各个临界处的现象。然而,当相互作用增大时,系统的性质变得复杂,需要更好的计算方案的出现。我们保留了用最低朗道能级规范基波函数叠加成体系总波函数的方案,因为它在我们结果获得的过程中富有成效。总之,旋转框架下的超冷玻色气体是复杂的,关于它们的研究是迷人的。在较弱的相互作用下,系统的基态为玻色–爱因斯坦凝聚态,当相互作用增加,则激发谱中出现旋子结构,与超流氦4类似的。然而,这样的结构随着相互作用增加变得逐渐不稳定。当相互作用继续增加时则会出现具有周期性构型的涡旋阵列。涡旋阵列的数目是与相互作用系数密切相关,而涡旋的大小与旋转频率有关。在较强的相互作用下,当涡旋的数目与粒子数目出现数量级的特殊关系时,预计会形成量子霍尔结晶相。
基金项目
国家自然科学基金面上项目(批准号:12174055),量子玻色气体中超固态奇异性质的理论研究。
附录

. a schematic diagram of a particle located at (x, y) performing gyration motion with (x, y) as the center of gyration
图a1. 位于(x, y)处的粒子以(x, y)为回旋中心做回旋运动示意图
如图a1,通常,做回旋运动的朗道单粒子哈密顿量可以描述为
(30)
这个哈密顿量(30)可以很好地描述一个质量为
的粒子做回旋运动的系统,其中粒子绝对坐标
。接下来,我们引入新的量子力学算符:
,这里,算符满足对易关系
。沿z方向的有效场强
。哈密顿量在新定义的量子力学算符下可以重写为
(31)
随后,定义一对产生和湮灭算符
(32)
于是,有
(33)
这里,回旋频率
。对于玻色系统,产生算符和湮灭算符满足对易关系:
。如果选取相对于回旋中心坐标
的相对坐标
,那么
(34)
因此,在朗道规范
下的哈密顿量(30)则可以进一步给出
(35)
由于沿y方向的动量算符与单粒子系统哈密顿对易
。可知,它们可以有共同的本征态。假设共同本征态是
,相应的本征方程给出
(36)
然后,将波函数分离变量,
。由于
(37)
于是可以得到关于y变量的非归一化的波函数
。此外,根据(34),回旋中心坐标
能表达为
(38)
产生和湮灭算符也可以表示为
(39)
于是可以发现
,可知x和
存在共同本征态,标记为
,得到
(40)
我们开始定义
(41)
进一步得到
(42)
因此可以求解方程(42)并得到归一化函数
(43)
继续下去,有
(44)
总之,在朗道规范下,归一化的单体朗道规范波函数能被表达为
(45)
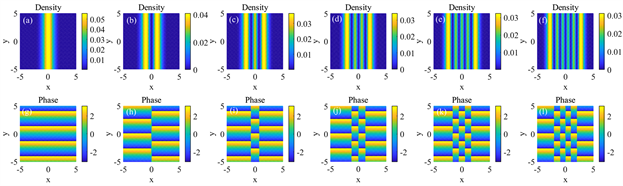
. the density distribution and phase distribution of the single landau gauge wave function at different n. from left to right they are n = 0 to n = 5
图a2. 单体朗道规范波函数在不同n时构成的密度分布和相位分布。从左到右分别是n = 0到n = 5
是厄密多项式。在图a2中,我们可以更形象的给出单体朗道规范波函数(45)在不同n时构成的密度分布和相位分布。特别地,取
,则朗道规范中最低朗道能级基态波函数可以描述为
(46)
notes
*通讯作者。